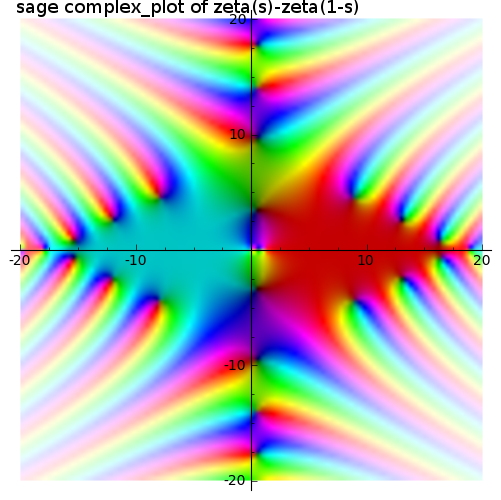
Are the 'semi' trivial zeros of $\zeta(s) \pm \zeta(1-s)$ all on the critical line?

Slightly off-topic : this article from Arxiv (in french) shows that zeros of functions f : s -> h(s) - h(1-s), where h is a meromorphic function satisfying appropriate growth conditions, are inclined to lie on the critical line, so this phenomenon is not specific to gamma functions.

I didn't check that the main result in the article apply to the function in GH's answer above.

If $\zeta(s)$ is nonzero, but $\zeta(s)\pm\zeta(1-s)=0$, then by the functional equation of the Riemann zeta function we have $$ \pi^{-\frac{s}{2}}\Gamma\left(\frac{s}{2}\right)\pm \pi^{-\frac{1-s}{2}}\Gamma\left(\frac{1-s}{2}\right)=0.$$ That is, your question is just the Riemann Hypothesis plus a more elementary one similar to your earlier question about the zeros of $\Gamma(s)\pm\Gamma(1-s)$. I would expect that the exact same techniques work here, i.e. one can show by known estimates for the gamma function that all nonreal solutions of the displayed equation lie on $\Re s=1/2$.

EDIT 1. To keep up with new developments I now expect that within the critical strip all nonreal solutions of the displayed equation lie on $\Re s=1/2$. Moreover, it seems reasonable to believe that there are no nonreal solutions with $|\Re s|$ sufficiently large.

EDIT 2. It follows from a generalized Rouché's theorem and Stirling's approximation that there are no nonreal solutions with $|\Re s|$ sufficiently large. More precisely, consider the rectangular contour $C_n$ with vertices $2n\pm it$ and $2n+2\pm it$, where $n>0$ is a large integer and $t>0$ is sufficiently large in terms of $n$. It suffices to show that along $C_n$ we have $$ \left|\pi^{-\frac{1-s}{2}}\Gamma\left(\frac{1-s}{2}\right)\right|<\left|\pi^{-\frac{s}{2}}\Gamma\left(\frac{s}{2}\right)\right|,$$ because this implies that inside $C_n$ there is precisely one solution of the above displayed equation (which must be real by the reflection principle). One can show that the right hand side divided by the left hand side is $ \gg n^{2n-\frac{1}{2}}(\pi e)^{-2n}$ on the vertical sides of $C_n$, while it is $\gg_n t^{2n-\frac{1}{2}}$ on the horizontal sides of $C_n$. The claim follows.

This might be a counter example to $\zeta(s)-\zeta(1-s)$.

Newton's method starting from $13 + 3i$ converges to $s \approx 13.16278786499+2.580464971850i$ which appears a zero.

[Added] A counterexample for $\zeta(s)+\zeta(1-s)$ appears $$ s \approx 14.870309115978233377 + 1.6450192905454179639i $$

[Added later] Per Agno's request the additional zeros found so far for $\zeta(s)-\zeta(1-s)$ are $16.478090665944547285 \pm 0.67940600947784773819i$ and $8.9909145336149198065 \pm 4.5105941406991465448i$

[Added later 2] The additional zeros of $\zeta(s)+\zeta(1-s)$ are $6.0002215061605926659 \pm 5.5128690434285266557$ and $11.248198934515946877 \pm 3.5349340823965337997$.

In all cases if $s$ is a zero so is $1-s$.

Here is a pari session with big precision:

\p 120
a=13.1627878649910358141631713461028903502674045760701701738298467140072119876746309296270651170803651644473445990732853741 + 2.58046497185066957108186074406714794119615081581034778843315640867385970134939303047779039837771630019890293928089781416*I
zeta(a)-zeta(1-a)
%2 = 3.667106168519458724 E-119 - 5.4882932400387681018240947190706996903 E-119*I

The starting value was opportunistically chosen from this plot. The colors are explained here