Ball to Ball Collision - Detection and Handling

To detect whether two balls collide, just check whether the distance between their centers is less than two times the radius. To do a perfectly elastic collision between the balls, you only need to worry about the component of the velocity that is in the direction of the collision. The other component (tangent to the collision) will stay the same for both balls. You can get the collision components by creating a unit vector pointing in the direction from one ball to the other, then taking the dot product with the velocity vectors of the balls. You can then plug these components into a 1D perfectly elastic collision equation.

Wikipedia has a pretty good summary of the whole process. For balls of any mass, the new velocities can be calculated using the equations (where v1 and v2 are the velocities after the collision, and u1, u2 are from before):

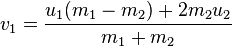
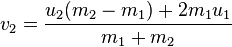
If the balls have the same mass then the velocities are simply switched. Here's some code I wrote which does something similar:

void Simulation::collide(Storage::Iterator a, Storage::Iterator b)
{
    // Check whether there actually was a collision
    if (a == b)
        return;

    Vector collision = a.position() - b.position();
    double distance = collision.length();
    if (distance == 0.0) {              // hack to avoid div by zero
        collision = Vector(1.0, 0.0);
        distance = 1.0;
    }
    if (distance > 1.0)
        return;

    // Get the components of the velocity vectors which are parallel to the collision.
    // The perpendicular component remains the same for both fish
    collision = collision / distance;
    double aci = a.velocity().dot(collision);
    double bci = b.velocity().dot(collision);

    // Solve for the new velocities using the 1-dimensional elastic collision equations.
    // Turns out it's really simple when the masses are the same.
    double acf = bci;
    double bcf = aci;

    // Replace the collision velocity components with the new ones
    a.velocity() += (acf - aci) * collision;
    b.velocity() += (bcf - bci) * collision;
}

As for efficiency, Ryan Fox is right, you should consider dividing up the region into sections, then doing collision detection within each section. Keep in mind that balls can collide with other balls on the boundaries of a section, so this may make your code much more complicated. Efficiency probably won't matter until you have several hundred balls though. For bonus points, you can run each section on a different core, or split up the processing of collisions within each section.

Well, years ago I made the program like you presented here.
There is one hidden problem (or many, depends on point of view):

• If the speed of the ball is too high, you can miss the collision.

And also, almost in 100% cases your new speeds will be wrong. Well, not speeds, but positions. You have to calculate new speeds precisely in the correct place. Otherwise you just shift balls on some small "error" amount, which is available from the previous discrete step.

The solution is obvious: you have to split the timestep so, that first you shift to correct place, then collide, then shift for the rest of the time you have.

You should use space partitioning to solve this problem.

Read up on Binary Space Partitioning and Quadtrees