Billiard dynamics under gravity

Here is the rather interesting result I get in Maple for a square of side 1 tilted at 30 degrees, acceleration of gravity = 1, initial position at the top left corner and moving horizontally with speed 1. This plot goes up to $t=300$. The trajectories appear to fill up a rectangular region (the top right boundary being an envelope).

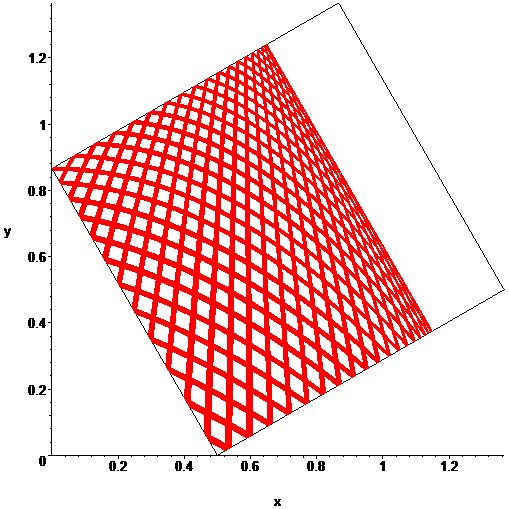
EDIT: And here's one with two envelopes, each parallel to an axis of the square.

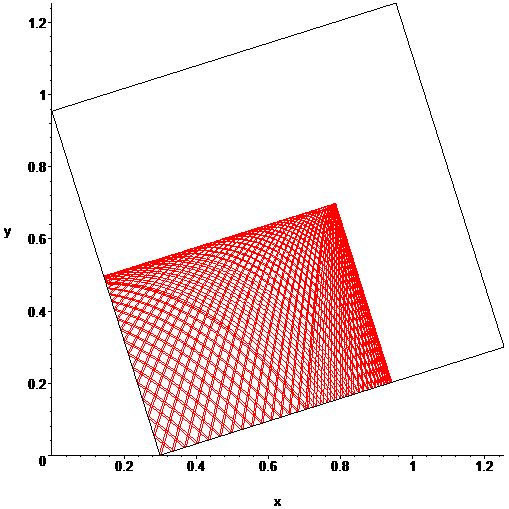
As fedja notes in the comments, the bounces off the right and left walls can be accounted for by unfolding the unit square into a horizontal strip, so the trajectories can be viewed as the parabolic arcs of an elastic ball that bounces off a floor and is constrained by a ceiling. We may as well start things at (0,0).

If the bouncing ball doesn't hit the ceiling -- say it maxes out at $(a,h)$ with $0 < h < 1$ -- then it simply traces a repeating set of parabolic arcs in the horizontal strip, with periodicity $2a$, in which case the billiard trajectory in the unit square is periodic if and only if $a$ is rational.

If the bouncing ball does hit the ceiling, say at $(a,1)$, then the trajectory thereafter is simply the reflection of the initial parabolic arc across the vertical line $x=a$. This again results in a repetition of arcs with period $2a$, so in either case (hitting the ceiling or not), the billiard trajectory in the unit square is periodic if and only if $a$ is rational.

The general case -- starting at an arbitrary point with an arbitrary initial speed and direction -- can be easily handled by following the initial parabolic arc to or from the floor and to or from its vertex or the ceiling, whichever is lower.

Nice picture, Robert. I think the way to understand this is the following: Unfold the square to the plane, keeping track of the "new" direction of gravity each time you do a reflection. In my picture, the direction of the gravitational field in each square is given by the black arrow. Now we need to understand the trajectory of a particle subject to this field. I've sketched (freehand and poorly!) the start of a trajectory in red. This gives us an explanation for the "boundary" in Robert's picture: since the vertical component of the gravitational force is constant along a horizontal strip and symmetric in the line going horizontally down the middle of my picture, if we start off with not too much vertical velocity, we'll never get higher than a given horizontal line (dotted, blue) or lower than the reflection of that line in the reflected squares. http://www.freeimagehosting.net/newuploads/a772c.png

Edit: picture didn't go up the first time. Giving it another shot