Consequences of eigenvector-eigenvalue formula found by studying neutrinos
The OP asks about generalisations and applications of the formula in arXiv:1908.03795.
$\bullet$ Concerning generalisations: I have found an older paper, from 1993, where it seems that the same result as in the 2019 paper has been derived for normal matrices (with possibly complex eigenvalues) --- rather than just for Hermitian matrices: On the eigenvalues of principal submatrices of normal, hermitian and symmetric matrices, by Peter Nylen, Tin-Yau Tam & Frank Uhlig (1993): theorem 2.2 (with the identification $b_{ij}=|u_{ij}|^2$ made at the very end of the proof).
A further generalisation to a signed inner product has been given in On the eigenvalues of principal submatrices of J-normal matrices (2011). In that case $b_{ij}=\epsilon_i\epsilon_j|u_{ij}|^2$, with $\epsilon_i=\pm 1$ the signature of the inner product: $(x,y)=\sum_i \epsilon_i x_i^\ast y_i$.
$\bullet$ Concerning applications: in the 1993 paper the theorem is used to solve the following problem: when does a normal $n\times n$ matrix $A$ with principal sub-matrices $M_j$ exist, given the sets of distinct (complex) eigenvalues $\lambda_i(A)$ of $A$ and $\lambda_k(M_j)$ of $M_j$. The answer is that the matrix $B$ with elements $$b_{ij}=\frac{\prod_{k=1}^{n-1}(\lambda_i(A)-\lambda_k(M_j))}{\prod_{k=1;k\neq i}^n(\lambda_i(A)-\lambda_k(A))}$$ should be unistochastic, meaning that $b_{ij}=|u_{ij}|^2$, where the matrix $U$ with elements $u_{ij}$ is the eigenvector matrix of $A$.
Since the 1993 paper is behind a paywall, I reproduce the relevant page:

A brief Mathematica file to test the formula is here.
Addendum: following up on the trail pointed out by Alan Edelman on Tao's blog: this 1966 paper by R.C. Thompson, "Principal submatrices of normal and Hermitian matrices", has the desired formula in the general case of normal matrices as Equation (15).
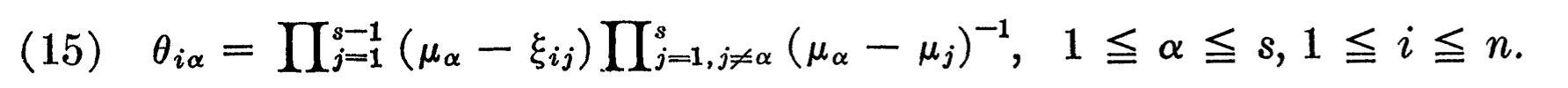
where $\theta_{ij}=|u_{ij}|^2$ when all eigenvalues $\mu_\alpha$ of $A$ are distinct (the $\xi_{ij}$'s are eigenvalues of $M_i$). The older papers mentioned in the comments below do not seem to have an explicit formula for $|u_{ij}|^2$.
Because this appears to be the earliest appearance of the eigenvector/eigenvalue identity, it might be appropriate to refer to it as "Thompson's identity",$^*$ as a tribute to professor Robert Thompson (1931-1995). It would fit in nicely with this quote from the obituary:
Among Thompson's many services to research was his help in dispelling the misinformed view that linear algebra is simple and uninteresting. He often worked on difficult problems, and as much as anyone, he showed that core matrix theory is laden with deeply challenging and intellectually compelling problems that are fundamentally connected to many parts of mathematics.
$^*$ "Thompson's identity" to distinguish from Thompson's formula
I want to add to the list of places where this identity has been used previously.
For a recent one, see arXiv:1710.02181 “State transfer in strongly regular graphs with an edge perturbation”. Equation (2) in Section 2 of this reads \[ \frac{\phi(X\setminus a,t)}{\phi(X,t)} = \sum_r \frac{(E_r)_{a,a}}{t-\theta_r} \] If the eigenvalue $\theta_r$ is simple. $E_r=z_rz_r^T$ and we have formula (2.3) in the pdf given in Carlos's reply. I have used it in a number of places in work on continuous quantum walks, e.g - Lemma 7.1 and Corollary 7.2 in arXiv:1011.0231 "When can perfect state transfer occur?"
It is used implicitly in my paper with Brendan McKay: "Spectral conditions for the reconstructibility of a graph", JCT B (30), 1981, 285–289.
We missed the connection to neutrinos :-(
There is an extensive treatment in Chapter 4 of my book "Algebraic Combinatorics". Chapman & Hall, New York, 1993.
Related identities appear in C. A. Coulson and H. C. Longuet-Higgins: "The electronic structure of conjugated systems I. General theory", Proc. Roy. Soc. London A191 (1947), 39–60. They prove that if $G$ is a graph with adjacency matrix $A$ and characteristic polynomial $\phi(G,t)$ and $\phi_{ij}(G)$ is the $ij$-entry of $\phi(G,t)(tI-A)^{-1}$, then \[ \phi_{ij}(G,t) = \sum_P \phi(G\setminus P,t) \] (where the sum is over all paths $P$ in $G$ from $i$ to $j$, and $G\setminus P$ is $G$ with all vertices in $P$ deleted). Further \[ \phi_{ij}(G,t) = \sqrt{\phi(G\setminus i,t)\phi(G\setminus j,t)-\phi(G,t)\phi(G\setminus {i,j},t)}. \]
The connection with eigenvectors arises because if $A=\sum_r \theta_r E_r$ is the spectral decomposition of $A$, then \[ \frac{\phi_{ij}(G,\theta_r)}{\phi'(G,\theta_r)} = (E_r)_{i,j}. \]
Essentially, the identity relates diagonal entries of spectral idempotents of Hermitian matrices to characteristic polynomials of principal submatrices. The off-diagonal entries are related to Green's functions, and I expect that there are papers in the physics literature where versions of the identity appear.