Evaluating an infinite sum related to $\sinh$

Here is a proof, surely not the simplest. Using $$\frac1{\sinh(n\pi)}=\frac{2e^{-\pi n}}{1-e^{-2\pi n}}=2\sum_{m\text{ odd}}e^{-mn\pi}$$ and $$2\sum_{n\text{ odd}}\frac{x^n}{n}=-2\ln(1-x)+\ln(1-x^2)=\ln\frac{1+x}{1-x},\qquad |x|<1,$$ we get that $$\sum_{n\text{ odd}}\frac1{n\sinh(n\pi)}=\sum_{m\text{ odd}}\ln\frac{1+e^{-m\pi}}{1-e^{-m\pi}}=\ln\prod_{m\text{ odd}}\frac{1+e^{-m\pi}}{1-e^{-m\pi}}.$$ This is the same as $\ln\frac{G_1}{g_1}$, where $G_N$ and $g_N$ are the class invariants as in Chapter 34 of Berndt: Ramanujan's notebooks, Part V. It is known (see same chapter) that $G_1=1$ and $(g_1G_1)^8(G_1^8-g_1^8)=\frac{1}{4}$. Hence $g_1=2^{-1/8}$, and the original sum equals $$\sum_{n\text{ odd}}\frac1{n\sinh(n\pi)}=\ln\frac{G_1}{g_1}=\frac{\ln 2}{8}.$$

In addition to GH's answer: this result can most easily be proved using Thompson–Lampard theorem of electrostatics: http://scitation.aip.org/content/aapt/journal/ajp/67/2/10.1119/1.19203 (A curious and useful theorem in two-dimensional electrostatics, by J. D. Jackson). From the concluding remarks of this paper:

For the mathematical physicist, the theorem elicits wonder and amusement. ‘‘Unbelievable’’ results such as $$\small \sum_{n \,even} \frac{8\sin^2{(n\pi a/2)}\sinh^2{(n\pi a/2)}}{n\sinh{(n\pi)}}+\sum_{n \,odd}\frac{8\cos^2{(n\pi a/2)}\cosh^2{(n\pi a/2)}}{n\sinh{(n\pi)}}=\ln{2} \tag{1}$$ valid for any $a$ ($0\le a<1$), and its special case ($a=0$), $$\sum_{n \,odd}\frac{8}{n\sinh{(n\pi)}}=\ln{2}, \tag{2}$$ are causes for wonder, as is the equivalent product, $$\prod\limits_{k=0}^\infty \left[\frac{1+e^{-(2k+1)\pi}}{1-e^{-(2k+1)\pi}}\right]^8=2.$$ The physicist, if not the mathematician, may view these relations as true curiosities, most easily proved by means of the very practical Thompson–Lampard theorem of electrostatics.

Completely mathematical proof of (1) (without using Thompson–Lampard theorem, but using Jacobi’s theta functions, as in the GH's proof) was given in http://scitation.aip.org/content/aip/journal/jmp/42/2/10.1063/1.1332123 (A mathematical proof of a result derived from the application of the Thompson–Lampard theorem of electrostatics, by D.A. Morales).

The special case (2) was evaluated in the paper http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=5245054 (A new theorem in electrostatics with applications to calculable standards of capacitance, by D. G. Lampard) and the evaluation is based on a more general result $$\sum_{n \,odd}\frac{1}{n\sinh{(n\pi\beta)}}=\frac{1}{2}\ln{\frac{\theta_3(0;e^{-\pi\beta})}{\theta_4(0;e^{-\pi\beta})}},$$ proved in the appendix of the paper.

this is not a proof – GH has given that – but I just want to note four more general series of this type listed in Andreas Dieckmann's extensive collection:

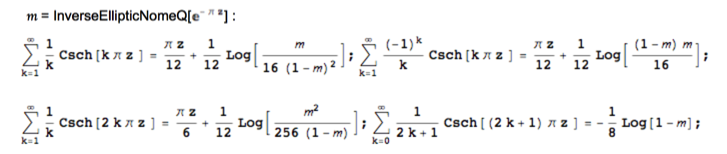
the OP's sum is the fourth series (or the difference of the first and second series) with $z=1\Rightarrow m=1/2$