Finding out nth fibonacci number for very large 'n'

You can save a lot time by use of memoization. For example, compare the following two versions (in JavaScript):

Version 1: normal recursion

var fib = function(n) {
  return n < 2 ? n : fib(n - 1) + fib(n - 2);
};

Version 2: memoization

A. take use of underscore library

var fib2 = _.memoize(function(n) {
  return n < 2 ? n : fib2(n - 1) + fib2(n - 2);
});

B. library-free

var fib3 = (function(){
    var memo = {};
    return function(n) {
        if (memo[n]) {return memo[n];}
        return memo[n] = (n <= 2) ? 1 : fib3(n-2) + fib3(n-1);
    };
})();

The first version takes over 3 minutes for n = 50 (on Chrome), while the second only takes less than 5ms! You can check this in the jsFiddle.

It's not that surprising if we know version 1's time complexity is exponential (O(2^N/2)), while version 2's is linear (O(N)).

Version 3: matrix multiplication

Furthermore, we can even cut down the time complexity to O(log(N)) by computing the multiplication of N matrices.

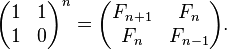
where F_n denotes the nth term of Fibonacci sequence.

You can use the matrix exponentiation method (linear recurrence method). You can find detailed explanation and procedure in this or this blog. Run time is O(log n).

I don't think there is a better way of doing this.