History of Mathematical Notation

For a quite extensive overview with many examples, you might want to check out The origins and development of mathematical notation. I also enjoyed reading Stephen Wolfram's take on Mathematical Notation – past and future, with a great variety of illustrations.

The OP asks specifically for the evolution of one formula, "to see the big picture". Here is one example, taken from Math through the ages:


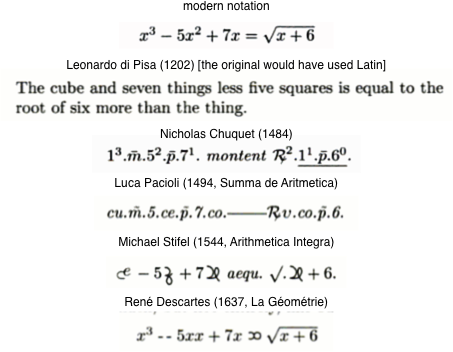
I think that the most complete source is still :

  • Florian Cajori (1859-1939), A History of Mathematical Notations (1928 - Dover reprint).

We can easily find there examples regarding the evolution of "algebraic" symbolism through the modern era :

  • §122 page 90 : Leonardo Piasano (Fibonacci) (c.1170 – c.1250), from Liber abaci

  • §130 page 101 : Nicolas Chuquet (c.1445 – c.1488), from Triparty en la science des nombres

  • §132 page 103 : Estienne de La Roche (1470–1530), from L'Arismetique (1520)

  • §134-on page 106 : Luca Pacioli (c.1447–1517), from Summa de arithmetica, geometria, proportioni et proportionalita (1494)

  • §140 page 117 : Gerolamo Cardano (1501 – 1576) ), from Artis Magnæ, Sive de Regulis Algebraicis Liber Unus (1545)

  • §151 page 139 : Michael Stifel (1487 – 1567), from Arithmetica integra (1544)

  • §162 page 154 : Simon Stevin (1548 – 1620), from De Thiende ('the art of tenths'), first published in Dutch in 1585 and translated into French as Disme

  • §170 page 169 : Leonard (c.1515–c.1559) and Thomas Digges (c.1546 – 1595) , from An Arithmetical Warlike Treatise Named Stratioticos (1579)

  • §176 page 181 : François Viète (1540 – 1603), from Zeteticorum libri quinque (1591)

  • §191 page 205 : René Descartes (1596 - 1650), from La Géométrie (1637).


"The big picture" that can be seen in Carlo Beenakker's example is

Rhetorical (verbal); Syncopated (abbreviated words); Symbolic.

However, this well-known picture is very algebra-oriented and does not say anything about the use of notations in say geometry as discussed here " The Shaping of Deduction in Greek Mathematics: A Study in Cognitive History " or as asked here Uppercase Point Labels in High-School Diagrams. Thus, at least for me, the interesting answers to OP questions would be those that are not related to algebra.

Tags:

Ho.History Overview

Related

Strongly real elements of odd order in sporadic finite simple groups A new result on the Diophantine equation $x^3 + y^3 +z^3 = 3$ Mahlo cardinal and hyper k-inaccessible cardinal Definition of étale (etc) for non-representable morphisms of algebraic stacks? Pullback along Frobenius morphism The intuition behind the Hilbert projective metric and the Perron Frobenius Theorem Which philosophy for reductive groups? Probability of two vectors lying in the same orthant Even Galois representations "mod p" Is there a similar theory as for symmetric polynomials, that deals with polynomials on the entries of matrices that are symmetric in both dimensions? What happened to the fourth paper in the series "On the classification of primitive ideals for complex classical Lie algebras" by Garfinkle? Relationship between the Lie functor applied to a Lie group action, and the fundamental vector field mapping?

Recent Posts