How can a day be exactly 24 hours long?

You can't calculate the length of a mean solar day just by taking the mean of the shortest & longest apparent solar days. That would work if the apparent day lengths varied in a simple linear fashion, but that's not the case.

From Wikipedia's article on the Equation of Time,

The equation of time describes the discrepancy between two kinds of solar time. [...] The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun, and mean solar time, which tracks a theoretical mean Sun with uniform motion.

This graph shows the cumulative differences between mean & apparent solar time:

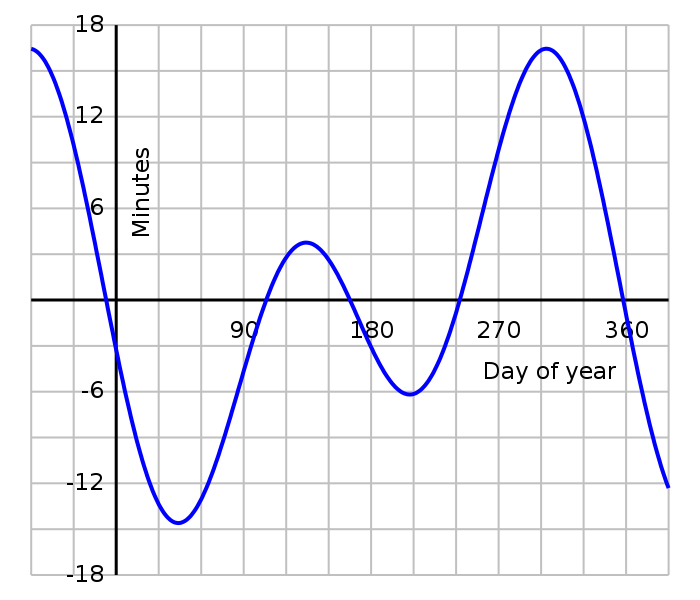
The equation of time — above the axis a sundial will appear fast relative to a clock showing local mean time, and below the axis a sundial will appear slow.

To correctly calculate the mean solar day length you need to integrate the apparent day lengths over the whole year. (And you need to decide exactly how to define the length of the year, which is a whole complicated story in its own right).

There are two primary causes of the Equation of Time.
1. The obliquity of the plane of Earth's orbit (the ecliptic plane), which is tilted approximately 23° relative to the equatorial plane. This tilt is also responsible for the seasons.
2. The eccentricity of Earth's orbit, which causes the Earth's orbital speed to vary over the year. The following graph shows how these two components combine to create the Equation of Time.

Equation of time (red solid line) and its two main components plotted separately, the part due to the obliquity of the ecliptic (mauve dashed line) and the part due to the Sun's varying apparent speed along the ecliptic due to eccentricity of the Earth's orbit (dark blue dash & dot line)

Please see the linked Wikipedia article for further details.

The average value of a distribution is not the average of its minimum and maximum. For example, the average value of (0,0,0,4) is 1, not 2. Earth's orbit eccentricity is not 0, nor the Moon's one, so your distribution of day duration is probably slightly asymetric, hence the 4 seconds discrepancy. Sum all day duration of a year, divide by the number of days, you will get a better value.

The original definition of an hour was 1/24th of a day, no matter how long the day was at the time. The durations you're quoting are only possible with the help of extremely modern definitions made possible by redefining the second (keeping the minute and hour fixed as 60 seconds, and 3600 seconds, respectively).