How do I iterate over Binary Tree?

Can you change it to Iteration instead of a recursion?

You can, using an explicit stack. Pseudocode:

private static void iterateall(BinaryTree foo) {
    Stack<BinaryTree> nodes = new Stack<BinaryTree>();
    nodes.push(foo);
    while (!nodes.isEmpty()) {
        BinaryTree node = nodes.pop();
        if (node == null)
            continue;
        System.out.println(node.node);
        nodes.push(node.right);
        nodes.push(node.left);
    }
}

But this isn’t really superior to the recursive code (except for the missing base condition in your code).

What you're looking for is a successor algorithm.

Here's how it can be defined:

First rule: The first node in the tree is the leftmost node in the tree.
Next rule: The successor of a node is:
- Next-R rule: If it has a right subtree, the leftmost node in the right subtree.
- Next-U rule: Otherwise, traverse up the tree
  - If you make a right turn (i.e. this node was a left child), then that parent node is the successor
  - If you make a left turn (i.e. this node was a right child), continue going up.
  - If you can't go up anymore, then there's no successor

As you can see, for this to work, you need a parent node pointer.

Example:

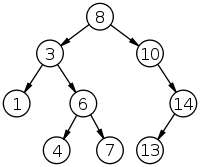
First rule: The first node in the tree is the leftmost node in the tree: (1)
Next-U rule: Since (1) has no right subtree, we go up to (3). This is a right turn, so (3) is next.
Next-R rule: Since (3) has a right subtree, the leftmost node in that subtree is next: (4).
Next-U rule: Since (4) has no right subtree, we go up to (6). This is a right turn, so next is (6).
Next-R rule: Since (6) has a right subtree, the leftmost node in that subtree is next: (7).
Next-U rule: Since (7) has no right subtree, we go up to (6). This is a left turn, so we continue going up to (3). This is a left turn, so we continue going up to (8). This is a right turn, so next is (8).
Next-R rule: Since (8) has a right subtree, the leftmost node in that subtree is next: (10).
Next-R rule: Since (10) has a right subtree, the leftmost node in that subtree is next: (13).
Next-U rule: Since (13) has no right subtree, we go up to (14). This is a right turn, so next is (14).
Next-U rule: Since (14) has no right subtree, we go up to (10). This is a left turn, so we continue going up to (8). This is a left turn, so we want to continue going up, but since (8) has no parent, we've reached the end. (14) has no successor.

Pseudocode

Node getLeftMost(Node n)
  WHILE (n.leftChild != NULL)
    n = n.leftChild
  RETURN n

Node getFirst(Tree t)
  IF (t.root == NULL) RETURN NULL
  ELSE
     RETURN getLeftMost(t.root);

Node getNext(Node n)
  IF (n.rightChild != NULL)
     RETURN getLeftMost(n.rightChild)
  ELSE
     WHILE (n.parent != NULL AND n == n.parent.rightChild)
        n = n.parent;
     RETURN n.parent;

PROCEDURE iterateOver(Tree t)
  Node n = getFirst(t);
  WHILE n != NULL
     visit(n)
     n = getNext(n)

Java code

Here's a simple implementation of the above algorithm:

public class SuccessorIteration {
    static class Node {
        final Node left;
        final Node right;
        final int key;
        Node parent;
        Node(int key, Node left, Node right) {
            this.key = key;
            this.left = left;
            this.right = right;
            if (left != null) left.parent = this;
            if (right != null) right.parent = this;
        }
        Node getLeftMost() {
            Node n = this;
            while (n.left != null) {
                n = n.left;
            }
            return n;
        }
        Node getNext() {
            if (right != null) {
                return right.getLeftMost();
            } else {
                Node n = this;
                while (n.parent != null && n == n.parent.right) {
                    n = n.parent;
                }
                return n.parent;
            }
        }
    }
}

Then you can have a test harness like this:

static Node C(int key, Node left, Node right) {
    return new Node(key, left, right);
}
static Node X(int key)             { return C(key, null, null);  }
static Node L(int key, Node left)  { return C(key, left, null);  }
static Node R(int key, Node right) { return C(key, null, right); }
public static void main(String[] args) {
    Node n =
        C(8,
            C(3,
                X(1),
                C(6,
                    X(4),
                    X(7)
                )
            ),
            R(10,
                L(14,
                    X(13)
                )
            )
        );
    Node current = n.getLeftMost();
    while (current != null) {
        System.out.print(current.key + " ");
        current = current.getNext();
    }
}

This prints:

1 3 4 6 7 8 10 13 14

How do I iterate over Binary Tree?

Example:

Pseudocode

Java code

See also

Tags:

Algorithm

Java

Recursion

Traversal

Binary Tree

Related

Recent Posts