How to get this integral's asymptotics?
$$I(\epsilon,B)=\int_0^{\infty}\frac{e^{-x}-1}{x^{2-\epsilon}}\frac{1}{B-i\pi/2-\log x}\,dx$$ $$\text{with}\;\;\epsilon=-\frac{A}{\log b-5/6}\in(0,1)\;\;\text{and}\;\;B=\log b<0$$
The limit $b\rightarrow 0^+$ corresponds to $\epsilon\rightarrow 0^+$, $B\rightarrow-\infty$ while the product $\epsilon B\rightarrow-A<0$ remains finite. That limit is governed by the small-$x$ behaviour of the integrand in $I(\epsilon,B)$, so we may expand $e^{-x}-1\rightarrow-x+{\cal O}(x^2)$ and calculate $$\lim_{\epsilon\rightarrow 0^+}I(\epsilon,-A/\epsilon)=\lim_{\epsilon\rightarrow 0^+}\int_0^{1}x^{\epsilon-1}\frac{1}{A/\epsilon+\log x+i\pi/2}\,dx=e^{-A}\left[-i\pi+\text{Ei}\,(A)\right],$$ with ${\rm Ei}(x)=-\int_{-x}^\infty t^{-1}e^{-t}\,dt$ the exponential integral function.
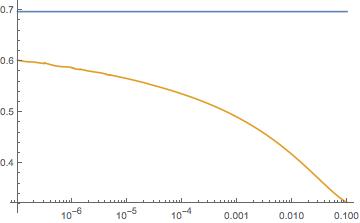
The curve below (gold) shows ${\rm Re}\,I$ as a function of $b$ for $A=1$; I was not able to push the numerical integration to smaller $b$, but the numerics is not inconsistent with the analytical result for the asymptote at $e^{-1}\,{\rm Ei}\,(1)=0.697$ (blue horizontal line).
The integral in question is
\begin{equation*}
I:=\int_0^\infty f(x)\,dx, \tag{1}
\end{equation*}
where
\begin{equation*}
f(x):=\frac{e^{-x}-1}{x^{2-\varepsilon}}\frac{1}{\ln(b/x)-i\pi/2},\quad
\varepsilon:=-\frac{A}{\ln b-5/6}\downarrow0.
\end{equation*}
Let
\begin{equation*}
C:=C_\varepsilon:=A-\tfrac56\,\varepsilon,
\end{equation*}
so that
\begin{equation*}
b=e^{-C/\varepsilon}.
\end{equation*}
We have
\begin{equation*}
\int_{b^{1/2}}^\infty f(x)\,dx
\sim\int_{b^{1/2}}^\infty \frac{e^{-x}-1}{x^{2-\varepsilon}}\frac{dx}{\ln(b/x)}
=\frac{J_1+J_2}{b^{1-\varepsilon}},
\end{equation*}
where
\begin{equation*}
J_1:=\int_{\varepsilon^{1/2}/b}^\infty \frac{1-e^{-by}}{y^{2-\varepsilon}}\frac{dy}{\ln y}
\le\int_{\varepsilon^{1/2}/b}^\infty \frac{dy}{y^{2-\varepsilon}}\frac{1}{\ln(\varepsilon^{1/2}/b)}
\ll\varepsilon^{1/2}b^{1-\varepsilon}=o(b^{1-\varepsilon})
\end{equation*}
and, with $u=\varepsilon\ln y$,
\begin{equation*}
J_2:=\int_{b^{-1/2}}^{\varepsilon^{1/2}/b} \frac{1-e^{-by}}{y^{2-\varepsilon}}\frac{dy}{\ln y}
\sim b \int_{b^{-1/2}}^{\varepsilon^{1/2}/b} \frac{dy}{y^{1-\varepsilon}}\frac{1}{\ln y}
= b \int_{C/2}^{C+\varepsilon\ln(\varepsilon^{1/2})}\frac{du}u\,e^u
\sim b(\text{Ei}(A)-\text{Ei}(A/2)).
\end{equation*}
It follows that
\begin{equation*}
\int_{b^{1/2}}^\infty f(x)\,dx
\to e^{-A}[\text{Ei}(A)-\text{Ei}(A/2)]. \tag{2}
\end{equation*}
Also, for
\begin{equation*}
g(x):=-\frac1{x^{1-\varepsilon}}\frac{1}{\ln(b/x)-i\pi/2},
\end{equation*}
we have
\begin{equation*}
\int_0^{b^{1/2}} |f(x)-g(x)|\,dx
\ll\int_0^{b^{1/2}} \frac{x^2}{x^{2-\varepsilon}}\frac{dx}{\pi/2}\to0. \tag{3}
\end{equation*}
Then, using the substitution $t=\varepsilon\ln(b/x)$, we have
\begin{equation*}
\int_0^{b^{3/2}} g(x)\,dx\sim
-\int_0^{b^{3/2}}\frac{dx}{x^{1-\varepsilon}}\frac{1}{\ln(b/x)}
=-e^{-C}\int_{C/2}^\infty \frac{dt}t\,e^{-t}=-e^{-C}\text{E}_1(C/2)\to
-e^{-A}\text{E}_1(A/2). \tag{4}
\end{equation*}
Further,
\begin{equation*}
\int_{b^{3/2}}^{b^{1/2}} g(x)\,dx=
\int_{b^{3/2}}^b g(x)\,dx+\int_b^{b^{1/2}} g(x)\,dx
=\int_{b^{1/2}}^1 g(bu)\,b\,du+\int_{b^{1/2}}^1 g(b/u)\,\frac{b\,du}{u^2}
=b\times\int_{b^{1/2}}^1 h(u)\,du,
\end{equation*}
where
\begin{equation*}
h(u):=g(bu)+g(b/u)/{u^2}
=-2i e^{C(1/\varepsilon-1)}e^t\,\frac{2\pi\cosh(\varepsilon t)+4i t \sinh(\varepsilon t)}{\pi^2+4t^2}
\end{equation*}
and $t:=-\ln u$.
(The latter identity is the key: note that $\Re g(x)$, as well as $\Re f(x)$, changes sign at $x=b$.)
So,
\begin{equation*}
\int_{b^{3/2}}^{b^{1/2}} g(x)\,dx=
-2i b e^{C(1/\varepsilon-1)}\int_0^{C/(2\varepsilon)}dt\,\frac{2\pi\cosh(\varepsilon t)+4i t \sinh(\varepsilon t)}{\pi^2+4t^2}. \tag{5}
\end{equation*}
Next,
\begin{equation*}
\int_0^{C/(2\varepsilon)}dt\,\frac{2\pi\cosh(\varepsilon t)}{\pi^2+4t^2}
\to\int_0^\infty dt\,\frac{2\pi}{\pi^2+4t^2}=\frac\pi2 \tag{6}
\end{equation*}
and
\begin{equation*}
\int_0^{C/(2\varepsilon)}dt\,\frac{4i t \sinh(\varepsilon t)}{\pi^2+4t^2}
=\int_0^{C/2}dz\,\frac{4i z \sinh z}{\varepsilon^2\pi^2+4z^2}
\to\int_0^{A/2}dz\,\frac{4i \sinh z}{4z}=i\,\text{shi}\frac A2, \tag{7}
\end{equation*}
where $\text{shi}$ is the hyperbolic sine integral function.
Collecting the pieces (1)--(7), we have
\begin{equation*}
I\to e^{-A}(\text{Ei}(A)-\text{Ei}(A/2))-e^{-A}\text{E}_1(A/2)-2i e^{-A} (\tfrac\pi2+i\,\text{shi}\tfrac A2)
=e^{-A}(\text{Ei}(A)-i\pi),
\end{equation*}
which is the same expression as the one obtained by Carlo Beenakker.