Design a One Instruction Set Computer!

XOISC

This OISC is based on Fokker's X-combinator which is defined as follows:

$$ X = \lambda f\ . f\ (\lambda g\ h\ x\ . g\ x\ (h\ x))\ (\lambda a\ b\ c\ . a) $$

If we acknowledge the fact that the SKI-calculus is Turing complete the above \$X\$-combinator is Turing complete as well. This is because \$S\$, \$K\$ and \$I\$ can be written in terms of \$X\$, like this:

$$ \begin{align} S &= X\ (X\ X) \\ K &= X\ X \\ I = S\ K\ K &= X\ (X\ X)\ (X\ X)\ (X\ X) \end{align} $$

How XOISC works

Internally XOISC has an (initially empty) stack, from there the instruction taking \$n\$ as an argument does the following:

Pop \$n\$ elements (functions \$ f_1 \dots f_N\$) from the stack, push \$f_1\ (f_2\ (\dots (f_N\ X) \dots ))\$

Once there are no more instructions left XOISC will push all command-line arguments (if any) to the stack, for example:

$$ [ \underbrace{s_1, \dots,\ s_M}_{\text{stack before}} ,\ \underbrace{a_1, \dots,\ a_N}_{\text{arguments}} ] $$

The final computation will be \$(\dots ((\dots (s_1\ s_2) \dots)\ s_M)\ a_1) \dots) a_N \$.

Since the one instruction in XOISC takes only one argument (memory offset) there is no reason to even use a name for that instruction. So a valid source file will constitute solely of integers separated by newlines or whitespaces, like for example:

0 0 2 0 1 0 1

Try it online!

Example

Let's take the above example (stack growing to the right):

$$ \begin{align} & \texttt{0} & \text{pop 0 and apply (ie. push single } X \text{)}: & \quad [X] \\ & \texttt{0} & \text{again simply push } X: & \quad [X,\ X] \\ & \texttt{2} & \text{pop 2 (} a,b \text{) and push } a\ (b\ X): & \quad [X\ (X\ X)] \\ & \texttt{0} & \text{simply push } X: & \quad [X\ (X\ X),\ X] \\ & \texttt{1} & \text{pop 1 (} a \text{) and push } a\ X: & \quad [X\ (X\ X),\ X\ X] \\ & \texttt{0} & \text{simply push } X: & \quad [X\ (X\ X),\ X\ X,\ X] \\ & \texttt{1} & \text{pop 1 (} a \text{) and push } a\ X: & \quad [X\ (X\ X),\ X\ X,\ X\ X] \end{align} $$

Finally evaluate the stack: \$((X\ (X\ X))\ (X\ X))\ (X\ X)\$ or with less parentheses \$X\ (X\ X)\ (X\ X)\ (X\ X)\$ which we recognize as the good old \$S\ K\ K\$ identity function.

Turing completeness

Proof idea

For XOISC to be Turing complete we need to be able to translate any (valid) interleaving of parentheses and \$X\$ combinators. This is possible because when popping, applying and pushing it does so in a right-associative manner (function application is left-associative).

To translate any such \$X\$ expression there is an easy way to do so: Always pop as many elements such that from the beginning of the current level of parentheses there will only be one element left.

As an example, the previously used expression: \$((X\ (X\ X))\ (X\ X))\ (X\ X)\$

to get \$X\$, we simply need a 0
next we're in a new level of parentheses, so we again only need a 0
now two parentheses close, so we need to pop 2 elements: 2
again we're in a new level of parentheses, so we need a 0
two parentheses, close so again a 2
and the same again

So we end up with a different (yet semantically equivalent) XOISC-program:

0 0 2 0 2 0 2 Try it online!

If we stay with this strategy we can easily transform any expression consisting of \$X\$ combinators to an XOISC program which only leaves a single function on the stack.

Formal proof

Given that the SKI-calculus is Turing complete, we need to show two things:

the \$X\$-combinator is a basis for the SKI-calculus
XOISC is able to represent any expression formed with the \$X\$ combinator

The first part - proving the three equalities in the introduction - is very tedious and space consuming, it's also not very interesting. So instead of putting it in this post, you can find here^*.

The second part can be proven by structural induction, though it's easier to prove a slightly stronger statement: Namely, for any expression formed by \$X\$-combinators there is a program that will leave that expression as a single expression on the stack:

There are two ways of constructing such an \$X\$ expression, either it's \$X\$ itself or it's \$f\ g\$ for some expressions \$f\$ and \$g\$:

The former one is trivial as 0 will leave \$X\$ on the stack as a single expression. Now we suppose that there are two programs (\$\texttt{F}_1 \dots \texttt{F}_N\$ and \$\texttt{G}_1 … \texttt{G}_K\$) that will leave \$f\$ and \$g\$ as a single expression on the stack and prove that the statement holds for \$f\ g\$ as well:

The program \$\texttt{F}_1 \dots \texttt{F}_N\ \texttt{G}_1 \dots \texttt{G}_{K-1}\ (\texttt{G}_K + 1)\$ will first generate \$f\$ on the stack and then it will generate \$g\$ but instead of only popping parts of \$g\$ it will also pop \$f\$ and apply it, such that it leaves the single expression \$f\ g\$ on the stack. ∎

Interpreter

Inputs

Since the untyped lambda calculus requires us to define our own data types for everything we want and this is cumbersome the interpreter is aware of Church numerals - this means when you supply inputs it will automatically transform numbers to their corresponding Church numeral.

As an example here's a program that multiplies two numbers: Try it online!

You can also supply functions as arguments by using De Bruijn indices, for example the S combinator \\\(3 1 (2 1)) (or λλλ(3 1 (2 1))). However it also recognizes the S, K, I and of course X combinator.

Output

By default the interpreter checks if the output encodes an integer, if it does it will output the corresponding number (in addition to the result). For convenience there's the -b flag which tells the interpreter to try matching a boolean instead (see the last example).

Assembler

Of course any low-level language needs an assembler that converts a high-level language to it, you can simply use any input (see above) and translate it to a XOISC-program by using the -a flag, try it online!^**

^{* In case the link is down, there's a copy as HTML comment in this post.}

^{** This results in a program that tests for primality, try it online!}

Draw

Draw is an OISC acting on a 2D grid, marking squares in a manner similar to the Wang B-machine. However, to keep the language as simple and OISC-y as possible, all instructions (of which there are a grand total of one) mark the square just stepped on, and, in order to be able to halt, stepping on a marked square terminates the program.

The program consists of a sequence of lines containing a line identifier (arbitrary string not including # or whitespace), two integers (x and y) and two more line identifiers (a and b).

The program runs as follows:
Starting at the line identified as start with the pointer pointing to position (0, 0), move the pointer by the amount given by x and y and mark the square the pointer is now on (unless the square is already marked, in which case execution terminates). Then, jump to line a if at least one of the directly adjacent squares is also marked, and to line b otherwise.

Interpreters are encouraged to output the final result of the grid as some sort of image, canvas, etc.

Turing-Completeness

Draw is Turing-complete as it is possible to compile a modified version (called Alternate) of a Minsky machine into the language.

Alternate acts similarly to a two-counter Minsky machine, but there is a large restriction placed on the commands: commands must alternate between targeting the first and second counter. To get around this modification, an additional command has been added: nop. This command doesn't change the targeted counter at all, which makes it possible to "pad" consecutive changes to one counter, satisfying the restriction outlined above. This also means that the register that is to be modified doesn't have to be given and, for any given instruction, can be directly inferred from the instructions from which execution can jump to it.

Example: this Minsky machine

1 inc A 2
2 inc A 3
3 dec A 3 4
4 halt

turns into this Alternate program:

1 inc 2
2 nop 3
3 inc 4
4 nop 5
5 dec 6 8
6 nop 5
7 halt
8 halt

This restriction is necessary due to the way that the eventual Draw program handles registers, which is to say that it doesn't differentiate between them at all. Instead, the Draw program simply copies the register that hasn't been changed by the preceding instruction, modifying it according to the instruction being executed.

Then, the Alternate program is directly translated into Draw as follows:

The program starts with this block.

start 0 0 a a
a 3 0 b b
b -3 1 c c
c 3 0 d d
d -3 2 e e
e 3 0 f f
f 3 -3 i1_a i1_a

inc, dec and nop are translated in almost the same way as each other. In all cases, there is no difference between changing the first or the second register (as explained above). Here is an increment, equivalent to inc 2:

i1_y 0 -2 i1_z i1_y
i1_z 3 -1 i1_a i1_a
i1_a -5 1 i1_b i1_b
i1_b 0 2 i1_c i1_c
i1_c 0 2 i1_d i1_e
i1_d 0 2 i1_d i1_f

i1_e 5 0 i2_z i2_y
i1_f 5 0 i2_z i2_y

Change the numbers in the i1_x parts to the index of the current instruction, and in the i2_x parts to the index of the next instruction to be executed.

The nop instruction can be translated as such:

i1_y 0 -2 i1_z i1_y
i1_z 3 -1 i1_a i1_a
i1_a -5 1 i1_b i1_b
i1_b 0 2 i1_c i1_c
i1_c 0 2 i1_d i1_e
i1_d 0 2 i1_d i1_f

i1_e 5 -2 i2_z i2_y
i1_f 5 -2 i2_z i2_y

This is a decrement:

i1_y 0 -2 i1_z i1_y
i1_z 3 -1 i1_a i1_a
i1_a -5 1 i1_b i1_b
i1_b 0 2 i1_c i1_c
i1_c 0 2 i1_d i1_e
i1_d 0 2 i1_d i1_f

i1_e 5 -2 i3_z i3_y
i1_f 5 -4 i2_z i2_y

i3_x refers to the instruction to be called if the counter is already 1.

Halt:

i1_y 0 0 0 0
i1_z 0 0 0 0

Change labels appropriately and simply chain everything together. Doing this for the example from above gives the Draw program in the repository from above.

Interpreters

There are currently two interpreters, both written in Python. They can be found on Draw's GitHub repository.

draw.py: This interpreter is meant for the command line and takes the program source as an argument. After every step, it outputs the command that was executed and the location of the instruction pointer; after the program halts, it prints the number of marked cells.
draw_golly.py: This version uses Golly for ~~exactly the wrong purpose~~ easier graphical output, taking the source via a popup box when starting the script. Golly can be a little finicky with Python, so make sure you have Python 2 installed (and don't mix 32-bit Golly with 64-bit Python or vice versa). Output is provided via Golly's builtin cell grid.

The following image is an example for output from the second interpreter. Running the example program in the repository gives this (or similar):

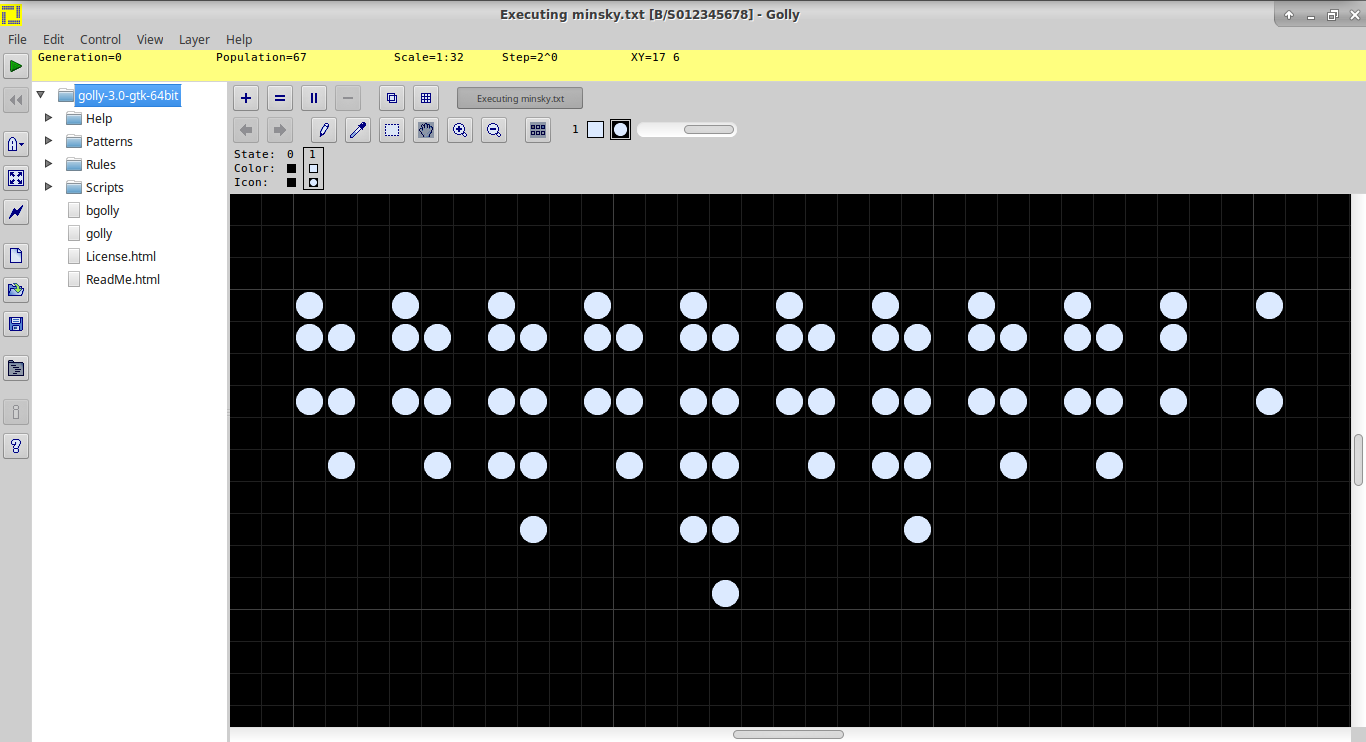
-3

Here's the gist.

Memory

Memory is a map of tapes, where the keys are strings and values are arbitrary-sized integers.

Additionally, there is a set of labels, where the program can jump to.

There is a stack, which contains the operands, which are strings.

There is an offset, which controls where in the memory's tapes it can access.

The One Instruction

-. First, it pops a string LABEL off the stack. If that LABEL is undefined as a label, it defines the label, and clears the source of that label (i.e. where it was pushed from) and the current instruction. Otherwise, it performs the following calculation, using the top two values, A and B:

if mem[A] < mem[B]:
    jump to LABEL
if mem[A] != mem[B]:
    mem[A]--
else:
    mem[B]++

Note that if there are excess arguments or insufficient arguments, the program will error out, showing the program's state.

The offset can be modified by accessing the value of ..

Example code

X-

i i X-
i i X-
i i X-
i i X-
i i X-
i i X-
i i X-

This sets variable i to 7, by incrementing 7 times.

X-

i i X-
i i X-
i i X-
LOOP-
    a a X-
    a a X-
    j i LOOP-

This multiplies i+1 by the constant 2.

Proof of Turing Completeness

Disregarding C++'s int sizes (that is, assuming they are infinite), -3 is Turing Complete by reduction to 3-cell brainfuck. I can disregard this size because there can be written an interpreter for -3 on a computer with infinite memory that has arbitrarily-large cells.

I also believe that any BCT can be written as a -3 program.