How do I can evaluate this integral: $\int_{1}^{\infty}\frac{y\cosh(yx)}{\sinh(y\pi)}dy$?
This may not be an answer to you mainly because there is perhaps no nice closed form, after all, according to what you like to call is "closed form" (an ever-evolving terminology depending on current knowledge of "elementary" functions).
Make the substitution $u=\pi y$ followed by $z=\frac{x}{\pi}$, and for convergence reasons assume $\vert z\vert<1$. Then, the given integral transforms to $$J:=\frac1{\pi^2}\int_{\pi}^{\infty}\frac{u\cosh(uz)}{\sinh u}du.$$ At this point, convert the hyperbolic functions into exponential and apply the geometric series $\frac1{1-e^{-2u}}=\sum_{k\geq0}e^{-2uk}$ to get (denoting $\alpha:=1-z$ and $\beta:=1+z$): \begin{align} J&=\frac1{\pi^2}\int_{\pi}^{\infty}\frac{u(e^{-u\alpha}-e^{-u\beta})}{1-e^{-2u}}du \\ &=\frac1{\pi^2}\sum_{k\geq0}\int_{\pi}^{\infty}u\left(e^{-u(2k+\alpha)}-e^{-u(2k+\beta}\right)du \\ &=\frac1{\pi^2}\sum_{k\geq0}\left(\frac{e^{-(2k+\alpha)\pi}}{(2k+\alpha)^2}+\frac{\pi e^{-(2k+\alpha)\pi}}{2k+\alpha}\right)- \frac1{\pi^2}\sum_{k\geq0}\left(\frac{e^{-(2k+\beta)\pi}}{(2k+\beta)^2}+\frac{\pi e^{-(2k+\alpha)\pi}}{2k+\beta}\right). \end{align} We recall the definition of the Lerch zeta function $$L(\lambda,a,s)=\sum_{k\geq0}\frac{e^{2\pi i\lambda k}}{(k+a)^s}.$$ As you can see, the integral $J$ may now be expressed as a linear combination of 4 Lerch values.
Caveat. Each of these 4 Lerch evaluations involve $i=\sqrt{-1}$, suggesting that one should be able (in theory) to combine (simplify) them in pairs since in the end $J$ should be real-valued.
I presume you are actually interested in this integral for some application, and then you might want a convenient expression --- Mathematica does evaluate it in closed form [*], as indicated in the comments, but this involves special functions and might not be of much practical use. Here is what I propose to do. Consider the integral with a variable lower bound,
$$I_u(x)=\int_{u}^{\infty}\frac{y\cosh(yx)}{\sinh(y\pi)}dy,\;\;u\geq 0,\;\;|x|<\pi.$$
The function for $u=0$ has a simple form,
$$I_0(x)=\frac{1}{2+2\cos x},$$
which is already quite close to the desired $I_1(x)$. We can improve by adding an offset of $-1/4$, as is evident from the plot: blue = $I_1$, orange = $I_0$, green = $I_0-\frac{1}{4}=\frac{1}{4}\tan^2(x/2)$
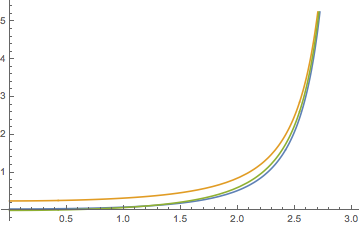
[*] For the record, after some massaging this is the Mathematica output for $I_1$, with $\Phi$ the Lerch transcendent:
$$I_1(x)= \frac{1}{2\cos^2(x/2)}\\ \quad+\sum_{+x,-x}\left[\frac{e^{\pi+x}}{\pi+x} \, _2F_1\left(1,\tfrac{x }{2 \pi }+\tfrac{1}{2};\tfrac{x}{2\pi} +\tfrac{3}{2};e^{2 \pi }\right)-\frac{e^{\pi+x}}{4 \pi ^2 } \Phi \left(e^{2 \pi },2,\tfrac{x }{2 \pi }+\tfrac{1}{2}\right)\right]$$
(the sum over $+x$ and $-x$ ensures that the result is an even function of $x$, as it should be)