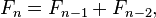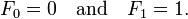In the Fibonacci sequence, is fib(0) 0 or 1 ?
The definition with Fib(0) = 1 is known as the combinatorial definition, and Fib(0) = 0 is the classical definition. Both are used in the Fibonacci Quarterly, though authors that use the combinatorial definition need to add a sentence of explanation. Benjamin and Quinn in Proofs that Really Count use f_n for the nth combinatorial Fibonacci number and F_n for the nth classical Fibonacci number. The combinatorial definition is good, not surprisingly for counting questions like "How many ways are there to walk up a flight of n steps, taking either one or two steps at a time?" When n is 0, there's one way to do it, not zero ways.
You're correct. The Fibonacci sequence is formally defined with seed values fib(0) = 0 and fib(1) = 1. This is a requirement for the rest of the sequence to be right (and not offset by one or anything).
In mathematics, the Fibonacci numbers, commonly denoted F_n, form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1.
In mathematics, the Fibonacci numbers, commonly denoted Fn, form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1.
Edit: I have to concede that there is another (much less common, and usually informal) way to define the sequence by seeding it with values 1 and 1, but this is not the conventional one by any means. It is certainly not preferred in all the formal mathematical definitions I’ve seen, like The On-Line Encyclopaedia of Integer Sequences.
From the Fibonacci number entry on Wikipedia:
In mathematics, the Fibonacci numbers are the following sequence of numbers:
By definition, the first two Fibonacci numbers are 0 and 1, and each remaining number is the sum of the previous two. Some sources omit the initial 0, instead beginning the sequence with two 1s.
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
with seed values