Infinity-categories vs Kan complexes
To define the fundamental $\infty$-groupoid as a Kan complex, you should take your homotopies to live on simplices rather than cubes. The resulting object is also called the singular simplicial set. The $0$-simplices are points, and the $1$-simplices are paths as expected. But the $2$-simplices are maps from a $2$-simplex into $X$ with the expected number of face maps, etc.
See http://ncatlab.org/nlab/show/fundamental+infinity-groupoid
I suspect your confusion arises in part because homotopies of paths are continuous maps $I^2 \to X$, while 2-morphisms in $\pi_{\lt \infty} X$ are continuous maps $\Delta^2 \to X$. That is, 2-morphisms are not strictly the same as homotopies of paths.
The dictionary between the two structures is not too bad:
A 2-morphism in $\pi_{\lt \infty} X$ is a homotopy of paths, where either the beginning or the end is fixed (or perhaps it is a homotopy to or from a constant path).
A continuous map $I^2 \to X$ can be viewed as a composite of two 2-morphisms in $\pi_{\lt \infty} X$. You end up using the diagonal $(0,0) \to (1,1)$ in the square to separate the two 2-morphisms, because the simplicial structure of $\Delta^1 \times \Delta^1$ has a diagonal 1-simplex.
I personally find it rather magical that among the sixteen 2-simplices in $\Delta^1 \times \Delta^1$, a pair of them pops out as non-degenerate - it is a rewarding computation.
More generally, higher dimensional cubes, viewed as products of the simplicial set $\Delta^1$, have canonical decompositions into nondegenerate simplices. The corresponding higher homotopies are composites of homotopies with various pieces held constant.
I think this should account for the discrepancy you see in the number of face maps.
Recall that Kan's first paper was cubical, but subsequent papers were simplicial as difficulties were found with the standard cubical category, in particular that cubical groups were not Kan, and the realisation of the cartesian product of cubical sets did not have the homotopy type of the product of the realisations. These deficiencies have been overcome by using cubical sets with connections (as developed in work with Higgins) in papers by A. Tonks, (JPAA 81}~(1) (1992) 83--87) and G. Maltsiniotis, (HHA 11~(2) (2009) 309--326.) respectively.
In my own work with Higgins, we have used cubical sets extensively see the book Nonabelian algebraic topology: filtered spaces, crossed complexes, cubical homotopy groupoids. One major reason for the success of cubical methods is that they can easily express multiple compositions:
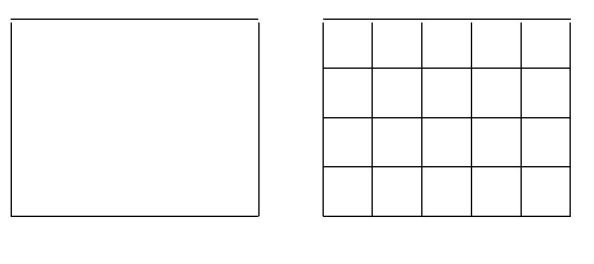
Thus in the above diagram, you can ask non mathematicians if they think that there should be some mathematics in which the left hand square can be regarded as some kind of composition of the right hand square, and they will happily agree. Fortunately, this language exists, as double categories, and in the case of the cubical singular complex we can also write down such compositions as a composition $[a_{ij}]$ of an array $(a_{ij})$ of cubes. (See Remark 13.1.11 of the above book.) So we have an "algebraic inverse to subdivision" and this can be used to obtain new local-to-global results. The notion of "connections" on cubical sets arose in trying to define "commutative cubes".
The main theorems of the book were envisaged cubically, and eventually realised, but I feel that simplicially or globularly they would not even be thought of. Indeed, this programme was, what should I say, not welcomed by some.
Further, cubes are excellent for homotopies and higher homotopies, because of the rule $I^m \times I^n \cong I^{m+n}$.
So my answer to the question on $\pi_2 X$ and how to see it simplicially is that one should look to the geometry and not try to force an intuition into an uncomfortable mode, especially when a convenient and natural mode is available, or at any rate, the pros and cons should be thought about carefully.
See also my answer to Generalized Categories for "Higher Homotopy Groupoids" .
Another recent reference is Modelling and Computing Homotopy Types:I.