Is there a koch circle?

Parts of the Mandelbrot set look like circles with smaller circles attached recursively:

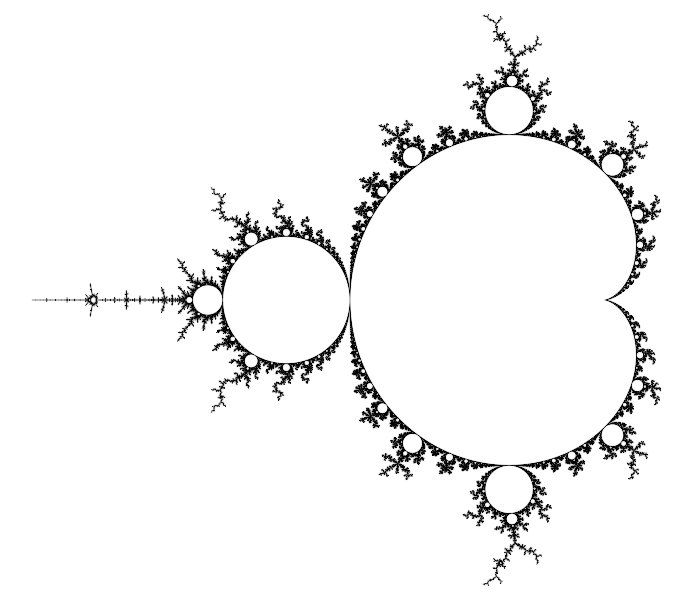
They aren't quite exact circles (except for the one centered at $-1+0i$), but the property that the radius of the smaller circle attached at rational angle $\frac{p}{q}$ measured in turns is approximately $q^2$ times smaller provides a way to construct a similar fractal from exact circles:

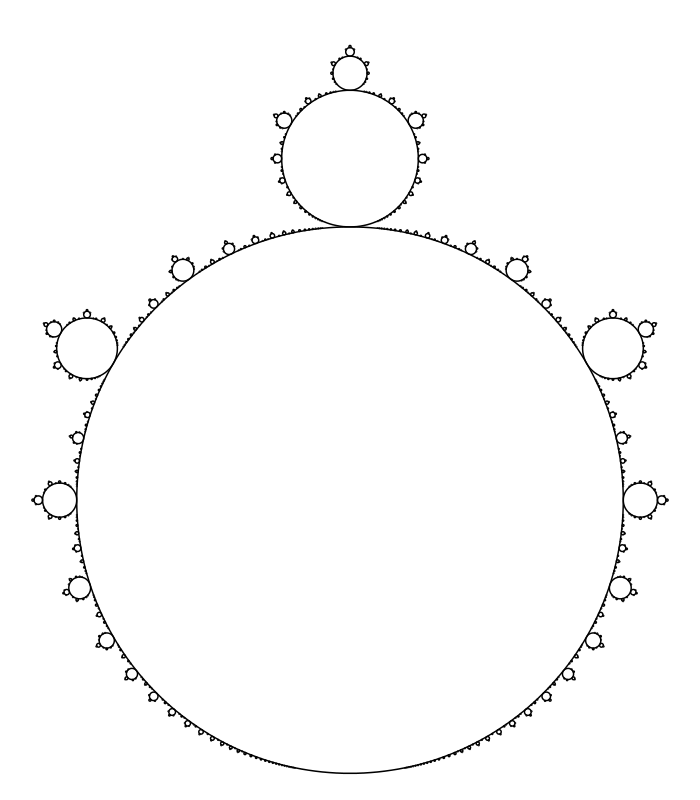
Haskell source code using the Diagrams library:

import Diagrams.Prelude
import Diagrams.Backend.SVG.CmdLine (defaultMain)

main
  = defaultMain
  $ diagram 1
  # rotateBy (-0.25)
  # pad 1.1
  # lw thin
  # bg white

power = 2

minimumRadius = 0.001

diagram radius
  | radius < minimumRadius = mempty
  | otherwise = circle radius <> mconcat
     [ diagram r
     # rotateBy (s - 0.5)
     # translate (r2 (rr * cos t, rr * sin t))
     | den <- [ 2 .. ceiling (sqrt (radius / minimumRadius)) ]
     , num <- [ 1 .. den - 1 ]
     , num `gcd` den == 1
     , let s = fi num / fi den
     , let t = 2 * pi * s
     , let r = radius / fi den ** power
     , let rr = radius + r
     ]
  where
    fi = fromInteger

Reducing the power makes the circles larger, but too low and they eventually overlap - in any case the power must be larger than one to ensure the circles actually do get smaller.

Is this any good?

It's the last frame in the animation for this answer.

Maybe the "Pharaoh's Breastplate" described by Mandelbrot.

Here plotted by Ken Monks