Lattice n-gons with ordered side lengths 1,2,3,...,n

There are indeed other such polygons. -- For example there is one for $n = 11$, as follows (the origin is in the lower left corner):

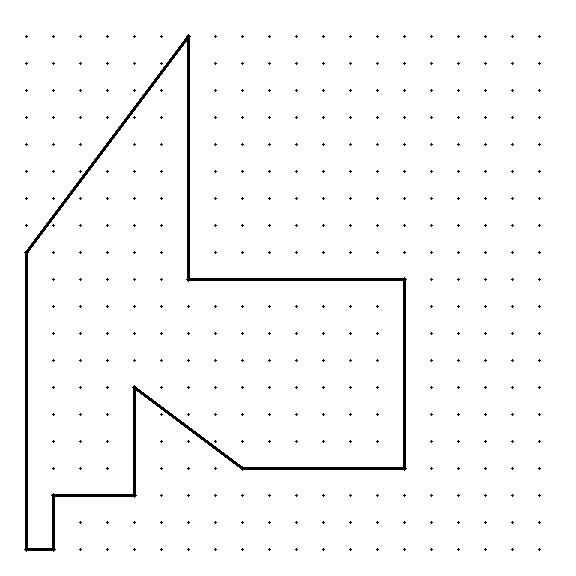
Also there is one for $n = 15$:

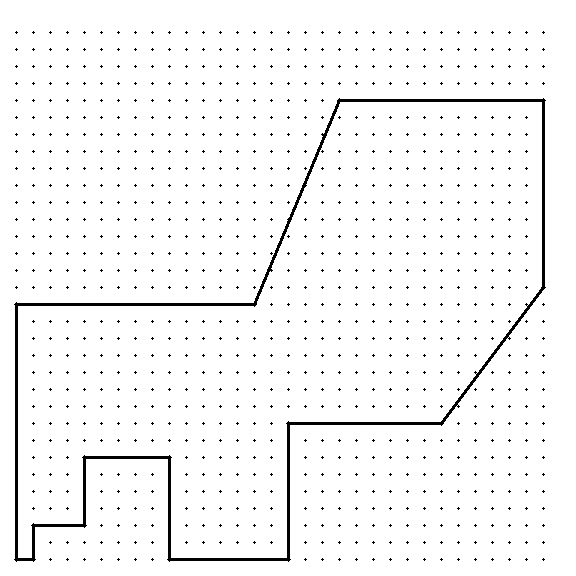
Further there are $21$ such polygons for $n = 16$. One of them is the following:

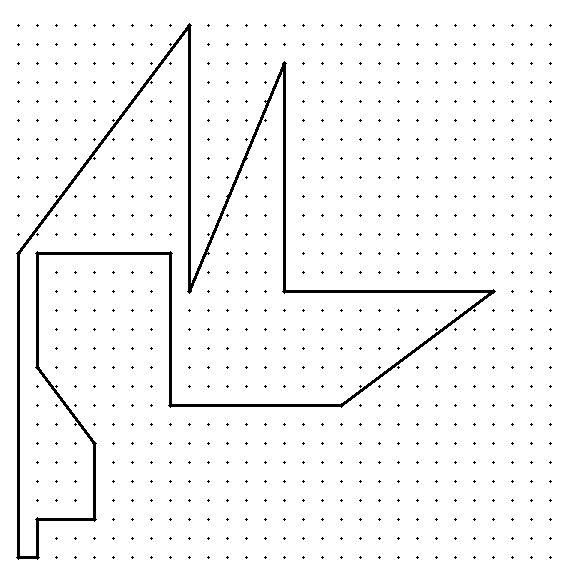
These polygons have been found with this GAP function.

There is one such polygon for $n = 8$, $n = 11$ and $n = 15$, each, there are $21$ such polygons for $n = 16$, and $225$ for $n = 19$. For all other $n < 20$ there are no such polygons.

The complete list for $n \leq 19$ in GAP-readable form can be found here.

Added on May 3, 2016: A zip file with *.png images of all $249$ polygons for $n \leq 19$ can be found here (545KB).

Added on May 4, 2016 (following a request in the comments): When leaving away the condition that the polygon is entirely in the first quadrant, we get $3$, $5$, $6$, $584$ and $882$ distinct polygons for $n = 8$, $n = 11$, $n = 12$, $n = 15$ and $n = 16$, respectively. A GAP-readable coordinate list can be found here, and a zip file with *.png images of all these $1480$ polygons can be found here (2.8MB).

If one looks at "isopaths", which are paths starting from the origin, taking steps of lengths 1,2,3,... in that order and always landing on a lattice point, without regard to self crossing or staying in the first quadrant, one sees exponentially many isopaths in a polynomial area, so there will be exponentially many paths beginning and ending on the same point.

If we now observe directed isopaths, which are noncrossing and constrained to lie in the lower part of the first quadrant ( mostly on or below the line y=x, with exceptions made to accommodate the first few steps ), again we have for n sufficiently large exponential growth in n inside a polynomially bounded space. This is because for most n there will be two or more choices of how to proceed to avoid self intersection, even if no movement had been made toward the opposite quadrant (decreasing both x and y).

If we now observe directed isopath tails (including steps of length m greater than 1 up to n inclusive) the same reasoning again shows exponentially many isopaths which are non intersecting and limited to a polynomially sized region. We can take a location (x,x) which admits several isopaths to it of length m-1 "from below", and similarly find several isopath tails which return to the origin "from above", giving the desired polygon. One can ensure non-intersection by picking n large enough and asking for a path from (x,x) back to (0,n) using steps of length m up to n-1. Since diagonal lengths are allowed (and the displacement takes the form related to one like (2MN, M^2 -N^2) ), I see no parity or modular obstructions (Oops! now I see one; thus n has to be even to admit such a polygon) when n gets sufficiently large, so each (Oops again! each allowed) lattice point in a certain region should be the arrival point of many isopaths and isopath tails.

Gerhard "Confident There Are Infinitely Many" Paseman, 2016.04.26.