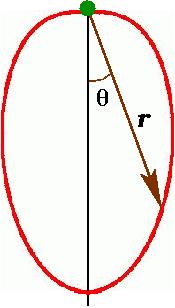
Maximal Gravity

This Physics quiz website by Yacov Kantor provides the solution in the February 2002 quiz. The optimal surface profile (with max gravity in the origin) in spherical and cylindrical coordinates for the solid of revolution is $r^2=z_0^2 \cos\theta$ and $(z^2+\rho^2)^{3/2}= z_0^2z$, respectively, $0\leq z\leq z_0$. The gravity in the origin is only 2.6% larger than the gravity on the surface of a spherical planet.