On the sum of uniform independent random variables

The answer is yes. Let $S_n:=\sum_{i=1}^n X_i$, $x\in\mathbb R$, $n=2,3,\dots$, and \begin{equation} G_n(x):=P(S_n/n\le x)=\frac1{n!}\,\sum_j(-1)^j\binom nj (nx-j)_+^n, \end{equation} where $u_+:=0\vee u$; cf. [Irwin--Hall distribution]. The summation here is over all integers $j$, with the usual convention that $\binom nj=0$ if $j\notin\{0,\dots,n\}$. Let \begin{equation} D_n(x):=G_{n+1}(x)-G_n(x). \end{equation} We have to show that $D_n(x)\ge0$ for $x\ge1/2$.

Clearly, $D_n$ is $n-1$ times continuously differentiable, $D_n=0$ outside $(0,1)$, and $D_n(1-x)=-D_n(x)$ (symmetry). For small $x>0$, one has $G_n(x)=\frac1{n!}\,n^nx^n>\frac1{(n+1)!}\,(n+1)^{n+1}x^{n+1}=G_{n+1}(x)$, whence $D_n(x)<0$, whence $D_n>0$ in a left neighborhood of $1$, with $D_n(1)=0$. Also, $D_n(1/2)=0$. So, it suffices to show that $D_n$ has no roots in $(1/2,1)$.

Suppose the contrary. Then, by the symmetry, $D_n$ has at least $3$ roots in $(0,1)$. Then, by the Rolle theorem, the derivative $G_n^{(n-1)}$ of $G_n$ of order $n-1$ has at least $3+n-1=n+2$ roots in $(0,1)$. This contradicts the fact (proved below) that, for each integer $j$ such that $n-1\ge j\ge\frac{n-1}2$, $D_n$ has exactly one root in interval $$h_{n,j}:=[\tfrac jn,\tfrac{j+1}n).$$

Indeed, take any $x\in[1/2,1]$. It is not hard to see that, for $j_x:=j_{n,x}:=\lfloor nx\rfloor$, \begin{equation} G_n^{(n-1)}(x)=n^{n-1}\sum_{j=0}^{j_x}(-1)^j\binom nj (nx-j) \end{equation}
\begin{equation} =\frac{n^{n-1}}{n-1}(-1)^{j_x}\binom n{j_x+1}({j_x}+1) ((n-1)x-{j_x}). \end{equation} Similarly, for $k_x:=j_{n+1,x}$, \begin{equation} G_{n+1}^{(n-1)}(x)=\frac{(n+1)^{n-1}}{2n(n-1)} (-1)^{k_x}\binom{n+1}{k_x+1}(k_x+1)P(n,k_x,x), \end{equation} where \begin{equation} P(n,k,x):=-2 k \left(n^2-1\right) x+k (k n-1)+n \left(n^2-1\right) x^2. \end{equation} Note that $k_x\in\{j_x,j_x+1\}$. Now we have to consider the following two cases.

Case 1: $k_x=j_x=j\in[\frac{n-1}2,n-1]$, which is equivalent to $x\in h'_{n,j}:=[\frac jn,\frac{j+1}{n+1})$. It also follows that in this case $j\ge n/2$. In this case, it is not hard to check that $D_n(x)$ equals $(-1)^j P_{n,j,1}(x)$ in sign, where \begin{equation} P_{n,j,1}(x):=2 j n^n (n-j)+x \left(-2 (n-1) n^n (n-j)-2 j (n+1)^n \left(n^2-1\right)\right)+j (n+1)^n (j n-1)+(n+1)^n \left(n^2-1\right) n x^2, \end{equation} which is convex in $x$. Moreover, $P_{n,j,1}(\frac jn)$ and $P_{n,j,1}(\frac{j+1}{n+1})$ each equals $2 n^n - (1 + n)^n<0$ in sign. So, $P_{n,j,1}<0$ and hence $D_n$ has no roots in $h''_{n,j}=[\frac jn,\frac{j+1}{n+1})$.

Case 2: $k_x=j+1$ and $j_x=j\in[\frac{n-1}2,n-1]$, which is equivalent to $x\in h''_{n,j}:=[\frac{j+1}{n+1},\frac{j+1}n)$. In this case, it is not hard to check that $D_n(x)$ equals $(-1)^{j+1} P_{n,j,2}(x)$ in sign, where \begin{equation} P_{n,j,2}(x):=(j+1) \left((n+1)^n (j n+n-1)-2 j n^n\right)+2 (j+1) \left((n-1) n^n-(n+1)^n \left(n^2-1\right)\right) x+n \left(n^2-1\right) (n+1)^n x^2, \end{equation} which is convex in $x$. Moreover, $P_{n,j,1}(\frac{j+1}n)$ and $-P_{n,j,1}(\frac{j+1}{n+1})$ each equals $2 n^n - (1 + n)^n<0$ in sign. So, $P_{n,j,2}$ has exactly one root in $h''_{n,j}$ and hence so does $D_n$.

Since the interval $h_{n,j}$ is the disjoint union of $h'_{n,j}$ and $h''_{n,j}$, $D_n$ has exactly one root in $h_{n,j}=[\tfrac jn,\tfrac{j+1}n)$, and the proof is complete.

Let's write $p_n(x)=P(S_n\le nx)$; we want to show that this increases in $n$ for fixed $x>1/2$. By conditioning on $X_{n+1}$, we obtain that $$ p_{n+1}(x) = \int_0^1 p_n\left( x+ \frac{x-y}{n} \right) \, dy = n\int_{x-(1-x)/n}^{x+x/n} p_n(t)\, dt . $$ So we're asking if $$ p_n(x) \le n \int_{x-(1-x)/n}^{x+x/n} p_n(t)\, dt \quad\quad\quad\quad (1) $$ By a Taylor expansion, the RHS of (1) equals $$ p_n(x) + p_n'(x) \frac{2x-1}{2n} + O(p_n''/n^2) , $$ so we'd be done if we could establish that $|p_n''(t)|\lesssim n p_n'(x)$ near $t=x$ with a sufficiently small implied constant. If we go back to the Irwin Hall distribution $F_n(a)=P(S_n\le a)$, then this becomes $|F_n''(t)|\lesssim F_n'(nx)$ near $t=nx$, and at least for large $n$, this is true since $F''_n$ doesn't vary much on an interval of length $L$, so it can't be much larger than $F'_n(x)/L$.

Comment: If we go back to (1), we see that there are competing effects. On the one hand, we're averaging over an asymmetric interval, giving preference to points $t>x$ where $p_n(t)>p_n(x)$, which is good. On the other hand, $p_n''<0$, which is bad, because this means that $p_n$ decreases more rapidly going to the left of $x$ than it increases going to the right.

Let me write $c=1/2+\delta$ and define $$P_n(\delta)\equiv \mathbb{P}\left[\sum_{i=1}^n X_i \leq n \cdot c\right].$$ Note that $P_n(0)=1/2$ and $P_n(1/2)=1$, irrespective of $n$.

It is convenient to work with the characteristic function of the Irwin-Hall distribution. I find the principal value integral $$\mathbb{P}\left[\sum_{i=1}^n X_i \leq n \cdot c\right]=\frac{1}{2}-\frac{1}{2\pi}\int_{-\infty}^\infty dt\,\frac{1}{(it)^{n+1}}\left(e^{it(1-c)}-e^{-ict}\right)^n,$$ which can be rewritten as $$P_n(\delta)=\frac{1}{2}+\frac{1}{\pi}\int_{0}^\infty dt\,\sin(2nt\delta)\,\frac{\sin^n t}{t^{n+1}}.$$

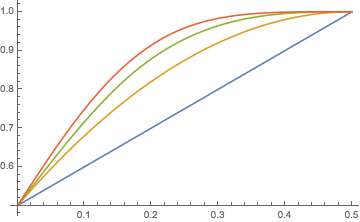
The plot shows $P_n(\delta)$ for $n=1,2,3,4$, from bottom curve to top curve. We need to demonstrate that this ordering of $P_n(\delta)$ with increasing $n$ holds for all $n$, so $P_n(\delta)$ increases with $n$ for all $\delta\in(0,1/2)$. I will attempt to prove this in several steps.

(I) $P_n(\delta)$ increases with $n$ near $\delta=0$.

For small $\delta$ the integral evaluates to

$$P_n(\delta)=\tfrac{1}{2}+2nC_n\delta+{\cal O}(\delta^3),$$

with the coefficient

$$C_n=\frac{1}{\pi}\int_0^\infty dt\,\frac{\sin^n t}{t^n}.$$

This integral over the $n$-th power of the sinc function is well-studied, we need to show that it decreases more slowly than $1/n$. For small $n$ this can be checked by explicit calculation, for large $n$ it follows from the asymptotic decay $C_n\propto 1/\sqrt n$. So the slope $P'_n(0)=2nC_n\propto \sqrt n$ is indeed an increasing function of $n$.

(II) $P_n(\delta)$ increases with $n$ near $\delta=1/2$.

This follows from a similar expansion around $\delta=1/2$, which shows that the first nonzero $p$-th order derivative $P_n^{(p)}(1/2)$ occurs for $p=n$. So near $\delta=1/2$ the function expands as

$$P_n(\delta)=1-(-1)^n A_n(\delta-1/2)^n+{\cal O}(\delta-1/2)^{n+1},\;\;A_n>0,$$

hence $P_n(\delta)$ increases with $n$ for $\delta$ just below $1/2$.

(III) Large-$n$ asymptotics

For $n\gg 1$ the sinc integral can be evaluated in closed form by means of the limit $$\lim_{n\rightarrow\infty}\left(\frac{\sin(t/\sqrt n)}{t/\sqrt n}\right)^n=\exp(-t^2/6)$$ so that $P_n(\delta)$ becomes asymptotically $$P_n(\delta)\rightarrow\frac{1}{2}+\frac{1}{\pi}\int_0^\infty dt\,\sin(2t\delta\sqrt n)\frac{1}{t}\exp(-t^2/6)=\frac{1}{2}+\frac{1}{2}\,{\rm Erf}\,(\delta\sqrt{6n}),$$ which has indeed a monotonically increasing $n$-dependence for each $\delta\in(0,1/2)$.

Note that we recover the $\sqrt n$ slope at $\delta=0$, $$P'_n(0)\rightarrow \sqrt{6n/\pi}\;\;\text{for}\;\;n\rightarrow\infty.$$ At $\delta=1$ the deviation from the exact limit $P_n(1/2)=1$ is exponentially small, $\propto\exp(-3n/2)/\sqrt n$.

The error function asymptotics is remarkably accurate already for small $n$, see the plot below for $n=3$ and $n=4$. For larger $n$ the exact and asymptotic curves are indistinguishable on the scale the figure.

---

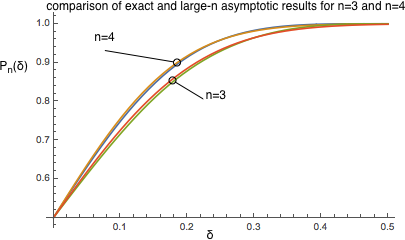
Bottom line.

I would think that the finite-$n$ analytics near $\delta=0$ and $\delta=1/2$, together with the large-$n$ asymptotics for the whole interval $\delta\in(0,1/2)$, goes a long way towards a proof of the monotonic increase with $n$ of $P_n(\delta)$, although some further estimation of the error in the asymptotics is needed to complete the proof. I am surprised by the fact that the large-$n$ asymptotics is so accurate already for $n=4$.