Should water at the scale of a cell feel more like tar?

There is a beautiful article (a write-up of a talk, actually), by E.M. Purcell, Life at low Reynolds number, that explains how bacteria swim.

Low Reynolds number is the technical way to phrase the statement in the OP that motion at that scale feels like moving in a tar pit. The governing equation is the linearized Navier-Stokes equation, a.k.a. the Stokes equation, which lacks the inertial $v\nabla v$ term. The linearity of the Stokes equation means that the swimming technique which we would use, moving arms or legs back and forth, will not work. Purcell calls this the "scallop theorem": opening and closing the shells of a scallop will just move the object back and forth, without net forward motion.
_{Inertia can still play a role on short time scales, as explained in Emergency cell swimming.}

The way bacteria move in the absence of inertia is the way a corkscrew enters a material upon turning, the cork screw being the flagellum. In fact, any nonsymmetrical object, when turned will propagate in a tar pit. Typical velocities are $1$ mm/min, as Purcell says: "Motion at low Reynolds number is very majestic, slow, and regular."

Here is a visualization of a sperm cell moving by rotating its flagellum (published just this week in Science Advances).

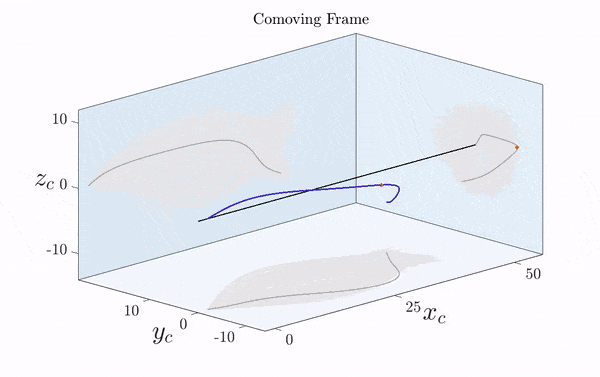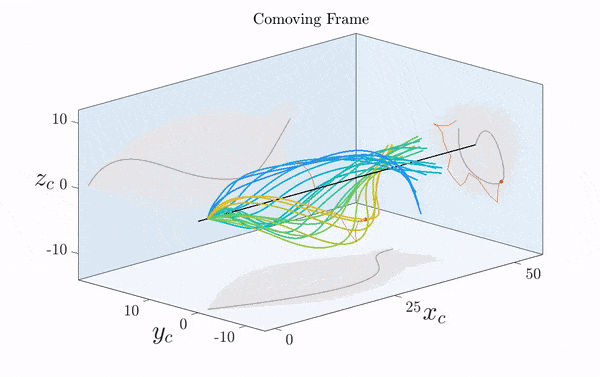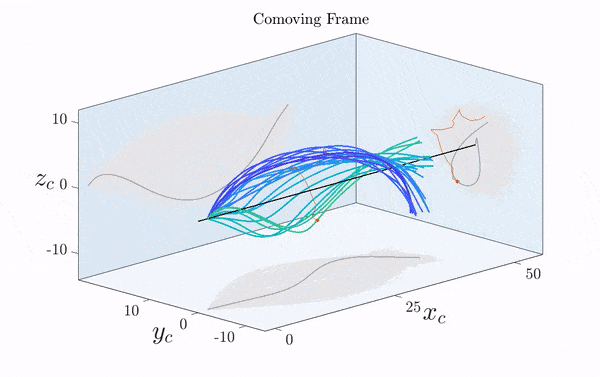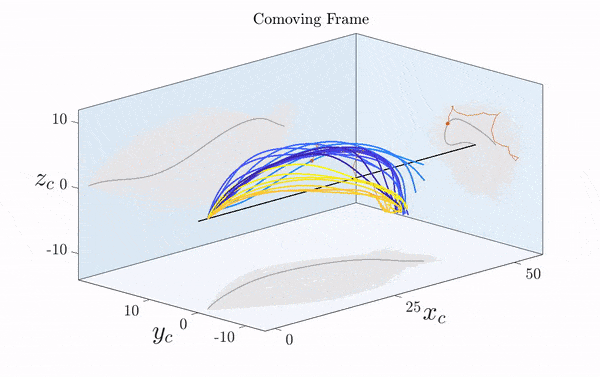
Note that the rotation is only clearly visible in three dimensions. Two-dimensional projections suggest a beating motion (first reported by Van Leeuwenhoek in the 17th century), which is not an effective means of propagation at low Reynolds number.

You may be interested in Shapere, A., and F. Wilczek. 1987. Self-propulsion at low Reynolds number. Phys. Rev. Lett. 58: 2051–2054 where they use gauge theory to describe micro-swimming. Because the Stokes equation - the infinite viscosity limit of Navier-Stokes - is linear, it allows us to define a connection for the principal G bundle: (located shapes) --> (unlocated shapes). Here G is the group of rigid motions of space, a located shape is (say) a volume-preserving embedding of the ball into usual 3-space, and the space of unlocated shapes is the quotient space of the space of located shapes by the action of G. Think of the ball as the cell (parmecium, E Coli, cyanobacterium, ..) which wants to move. A swimming stroke is then a loop in the space of unlocated shapes. The resulting holonomy for the Stokes connection is computed by solving the Stokes equation with zero boundary data at infinity. Shapere in his thesis estimates the curvature at the embedding which is a round ball, and thereby investigates ``infinitesimal swimming motions''. Some of this story can also be found in my book, A Tour of SubRiemannian Geometry.