What is (approximately) the expected value of $X\log{ X}$ where $X$ is binomial (or Poisson)?
$\newcommand{\ep}{\varepsilon} $ Let $X$ be any nonnegative random variable (r.v.) with finite mean $\mu>0$ and variance $\sigma^2<\infty$. For any real $u>0$, we have $\ln\frac xu\le\frac xu-1$ for all real $x>0$, whence $x\ln x\le\frac{x^2}u+x\ln\frac ue$ and \begin{equation*} EX\ln X\le\frac{EX^2}u+EX\ln\frac ue=\frac{\sigma^2+\mu^2}u+\mu\ln\frac ue. \end{equation*} Choosing here $u=u_{\mu,\sigma^2}:=\frac{\sigma^2+\mu^2}\mu[>\mu]$, we have \begin{equation*} EX\ln X\le B(\mu,\sigma^2):=\mu\ln\frac{\sigma^2+\mu^2}\mu. \tag{1} \end{equation*} On the other hand, by Jensen's inequality for the convex function $x\mapsto x\ln x$, \begin{equation*} EX\ln X\ge B(\mu):=\mu\ln\mu. \tag{2} \end{equation*}
If now $Y$ is a nonnegative r.v. such that $P(Y=u_{\mu,\sigma^2})=\mu/u_{\mu,\sigma^2}=1-P(Y=0)$, then $EY=\mu$ and $Var\,Y=\sigma^2$, and $EY\ln Y=B(\mu,\sigma^2)$. So, the upper bound $B(\mu,\sigma^2)$ on $EX\ln X$ is exact. Clearly, for $X=\mu$, the lower bound $B(\mu)$ on $EX\ln X$ is also exact.
In the particular case when (say) $X$ has the Poisson distribution with parameter $\lambda$, then (1) and (2) become \begin{equation*} \lambda\ln\lambda\le EX\ln X\le\lambda\ln(1+\lambda). \tag{3} \end{equation*} If $\lambda$ is large (which seems relevant to your case), then the upper and lower bounds on $EX\ln X$ in (3) are asymptotically equivalent to each other and hence asymptotically tight.
More generally, for the upper bound (1) and lower bound (2) on $EX\ln X$ to be asymptotically equivalent to each other and hence asymptotically tight, it is enough that $\sigma^2$ and $\mu$ vary in any such way that $\sigma^2=o(\mu^2)$ and $\mu$ be greater than $1$ and bounded away from $1$: \begin{equation*} \sigma^2=o(\mu^2)\quad\text{and}\quad \exists\ep>0\ \mu\ge1+\ep. \tag{4} \end{equation*} Indeed, then \begin{equation*} 0\le\frac{B(\mu,\sigma^2)}{B(\mu)}-1=\frac{\ln(1+\sigma^2/\mu^2)}{\ln\mu} \le\frac{\sigma^2/\mu^2}{\ln(1+\ep)}=o(1). \end{equation*} In particular, if $X$ has the binomial distribution with parameters $n$ and $p$, "for large $n$ and small (but fixed) $p$" (as in the OP), then (4) will hold, so that the upper and lower bounds on $EX\ln X$ in (1) and (2) will be asymptotically equivalent to each other and hence asymptotically tight. (Cf. the comment by Will Sawin.)
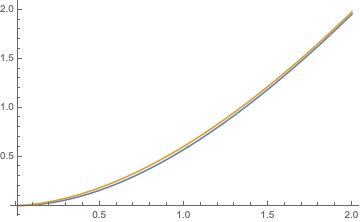
An integral approximation may be useful. Taking a Poisson distribution for $X$ with intensity $\lambda=np$, I approximate $$E_\lambda(X\log X)=\sum_{k=1}^\infty \lambda^k e^{-\lambda}\frac{k\log k}{k!}$$ by the integral $$I(\lambda)=\int_{1}^\infty \lambda^x e^{-\lambda}\frac{x\log x}{\Gamma(x+1)}\,dx.$$ The agreement, blue for $E_\lambda$, gold for $I(\lambda)$ is quite reasonable (see plot). Unfortunately, the integral does not simplify further.