What's the "actual" shape of a black hole accretion disk?

The "shape" of an accretion disc is the spatial profile of the gas density $\rho$ at a given time $t$. Here is a recent calculation, arXiv:1810.0083. This image shows what a distant observer, outside of the event horizon, would measure. Matter is falling into the black hole without ever crossing the event horizon, falling ever more slowly as it approaches the horizon.

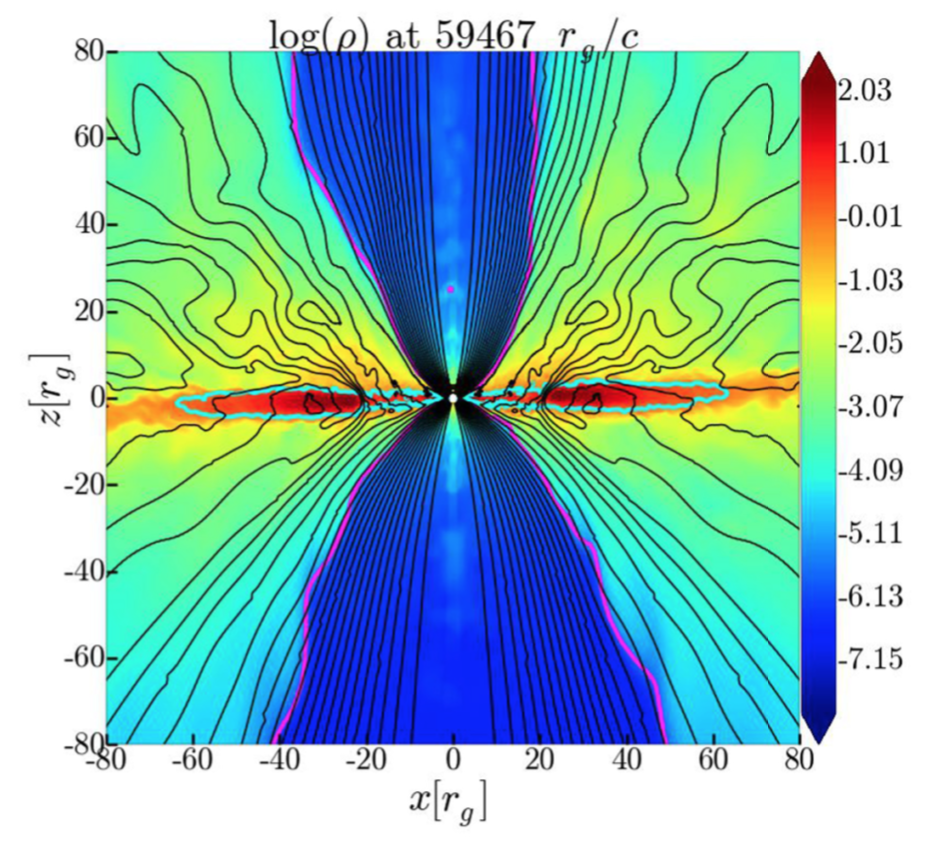
The density profile is shown on a logarithmic color scale (high density = red = $10^2$ g/cm$^3$, low density = blue = $10^{-7}$ g/cm$^3$), at a time $t=59\cdot 10^3 r_g/c$ after core collapse, with $r_g=GM/c^2$ the gravitational radius of the black hole (one half the Schwarzschild radius, which is the radius of the event horizon, of order $10^{13}$ m). The profile is a slice through the $x$–$z$ plane, when the $z$-axis is aligned with the rotational axis of the spinning black hole. (The density is rotationally symmetric in the $x$–$y$ plane.) The black lines are magnetic field lines.

The blue channel of relatively low density at the center appears because the lack of centrifugal forces along the rotational $z$-axis allows the gas to accrete much more readily than along the equatorial $x$–$y$ plane.

This is not really a complete answer, but would not have fit in a comment. Your description of the topology and the time slices contains some incorrect assumptions.

Let's take the simplest example of a black hole spacetime, which is the Schwarzschild spacetime (a black hole with zero charge and zero angular momentum). This spacetime is split into interior and exterior regions, with an event horizon in between. The event horizon is a null surface, not a timelike surface, so it doesn't act like a stationary boundary. It would be more accurate to think of it as if it were moving at the speed of light. (In the maximal analytic extension of the spacetime, there are actually two more regions, for a total of four, but these are not present in a black hole that forms by gravitational collapse.)

The exterior is stationary, meaning that it has a timelike Killing vector. An observer whose world-line is parallel to this vector observes a gravitational field that doesn't change over time, and can be considered to be at rest relative to the black hole. Because the Schwarzschild spacetime is also not rotational, such observers can synchronize their clocks, and we therefore have a preferred time foliation. However, this preferred time foliation does not exist for rotating black holes, which are what really exist in our universe. (The simulation in the OP is of a rotating black hole.)

But the interior region is not stationary. Therefore the preferred time foliation can't be extended into the interior. What this tells us is that there is never any well-defined way to talk about what is happening "now" inside a black hole. You can extend your spacelike surface of simultaneity into the interior, but there is no preferred way to do so. We can say that the infalling matter never reaches the horizon, but we can also say that it does. (According to an infalling observer, the matter passes through the horizon and reaches the singularity in milliseconds in the case of a solar-mass black hole.) I would interpret this as meaning that your question doesn't actually have a meaningful answer if you try to talk about anything but the exterior region.

I can imagine that in a given instant the whole picture is a leaf of a constant time foliation of spacetime (does such foliation exist in the case of a black hole?), which is a Riemannian manifold diffeomorphic to 3-space (minus the singularity).

The singularity is analogous to a spacelike surface, not a timelike one. A spacelike surface of simultaneity can be chosen either to intersect the singularity or not to intersect it. Therefore there are at least two different topologies possible for a surface of simultaneity.

Are light rays geodesics also for the induced Riemannian metric on the constant-time slices?

This question only makes sense on the exterior (and only for a non-rotating black hole), where there is a preferred foliation. There you can project out the time dimension. In that region, I think the answer is no. Geodesics of the spacetime are in general not geodesics after this type of projection. For example, the orbit of the earth is an ellipse under this type of projection, and that's not a geodesic of the spatial metric. I think it's pretty easy to see why we shouldn't expect the geodesic property to be preserved under projection. Different spacetime geodesics can be tangent to one another after projection, and you can't have different geodesics with the same tangent vector where they intersect.