What to use for flow free-like game random level creation?

Updated answer: I implemented a new generator using the idea of "dual puzzles". This allows much sparser and higher quality puzzles than any previous method I know of. The code is on github. I'll try to write more details about how it works, but here is an example puzzle: enter link description here

Old answer: I have implemented the following algorithm in my numberlink solver and generator. In enforces the rule, that a path can never touch itself, which is normal in most 'hardcore' numberlink apps and puzzles

First the board is tiled with 2x1 dominos in a simple, deterministic way. If this is not possible (on an odd area paper), the bottom right corner is left as a singleton.
Then the dominos are randomly shuffled by rotating random pairs of neighbours. This is is not done in the case of width or height equal to 1.
Now, in the case of an odd area paper, the bottom right corner is attached to one of its neighbour dominos. This will always be possible.
Finally, we can start finding random paths through the dominos, combining them as we pass through. Special care is taken not to connect 'neighbour flows' which would create puzzles that 'double back on themselves'.
Before the puzzle is printed we 'compact' the range of colours used, as much as possible.
The puzzle is printed by replacing all positions that aren't flow-heads with a .

My numberlink format uses ascii characters instead of numbers. Here is an example:

$ bin/numberlink --generate=35x20
Warning: Including non-standard characters in puzzle

35 20
....bcd.......efg...i......i......j
.kka........l....hm.n....n.o.......
.b...q..q...l..r.....h.....t..uvvu.
....w.....d.e..xx....m.yy..t.......
..z.w.A....A....r.s....BB.....p....
.D.........E.F..F.G...H.........IC.
.z.D...JKL.......g....G..N.j.......
P...a....L.QQ.RR...N....s.....S.T..
U........K......V...............T..
WW...X.......Z0..M.................
1....X...23..Z0..........M....44...
5.......Y..Y....6.........C.......p
5...P...2..3..6..VH.......O.S..99.I
........E.!!......o...."....O..$$.%
.U..&&..J.\\.(.)......8...*.......+
..1.......,..-...(/:.."...;;.%+....
..c<<.==........)./..8>>.*.?......@
.[..[....]........:..........?..^..
..._.._.f...,......-.`..`.7.^......
{{......].....|....|....7.......@..

And here I run it through my solver (same seed):

$ bin/numberlink --generate=35x20 | bin/numberlink --tubes
Found a solution!
┌──┐bcd───┐┌──efg┌─┐i──────i┌─────j
│kka│└───┐││l┌─┘│hm│n────n┌o│┌────┐
│b──┘q──q│││l│┌r└┐│└─h┌──┐│t││uvvu│
└──┐w┌───┘d└e││xx│└──m│yy││t││└──┘│
┌─z│w│A────A┌┘└─r│s───┘BB││┌┘└p┌─┐│
│D┐└┐│┌────E│F──F│G──┐H┐┌┘││┌──┘IC│
└z└D│││JKL┌─┘┌──┐g┌─┐└G││N│j│┌─┐└┐│
P──┐a││││L│QQ│RR└┐│N└──┘s││┌┘│S│T││
U─┐│┌┘││└K└─┐└─┐V││└─────┘││┌┘││T││
WW│││X││┌──┐│Z0││M│┌──────┘││┌┘└┐││
1┐│││X│││23││Z0│└┐││┌────M┌┘││44│││
5│││└┐││Y││Y│┌─┘6││││┌───┐C┌┘│┌─┘│p
5││└P│││2┘└3││6─┘VH│││┌─┐│O┘S┘│99└I
┌┘│┌─┘││E┐!!│└───┐o┘│││"│└─┐O─┘$$┌%
│U┘│&&│└J│\\│(┐)┐└──┘│8││┌*└┐┌───┘+
└─1└─┐└──┘,┐│-└┐│(/:┌┘"┘││;;│%+───┘
┌─c<<│==┌─┐││└┐│)│/││8>>│*┌?│┌───┐@
│[──[└─┐│]││└┐│└─┘:┘│└──┘┌┘┌┘?┌─^││
└─┐_──_│f││└,│└────-│`──`│7┘^─┘┌─┘│
{{└────┘]┘└──┘|────|└───7└─────┘@─┘

I've tested replacing step (4) with a function that iteratively, randomly merges two neighboring paths. However it game much denser puzzles, and I already think the above is nearly too dense to be difficult.

Here is a list of problems I've generated of different size: https://github.com/thomasahle/numberlink/blob/master/puzzles/inputs3

I think you'll want to do this in two steps. Step 1) find a set of non-intersecting paths that connect all your points, then 2) Grow/shift those paths to fill the entire board

My thoughts on Step 1 are to essentially perform Dijkstra like algorithm on all points simultaneously, growing together the paths. Similar to Dijkstra, I think you'll want to flood-fill out from each of your points, chosing which node to search next using some heuristic (My hunch says chosing points with the least degrees of freedom first, then by distance, might be a good one). Very differently from Dijkstra though I think we might be stuck with having to backtrack when we have multiple paths attempting to grow into the same node. (This could of course be fairly problematic on bigger maps, but might not be a big deal on small maps like the one you have above.)

You may also solve for some of the easier paths before you start the above algorithm, mainly to cut down on the number of backtracks needed. In specific, if you can make a trace between points along the edge of the board, you can guarantee that connecting those two points in that fashion would never interfere with other paths, so you can simply fill those in and take those guys out of the equation. You could then further iterate on this until all of these "quick and easy" paths are found by tracing along the borders of the board, or borders of existing paths. That algorithm would actually completely solve the above example board, but would undoubtedly fail elsewhere .. still, it would be very cheap to perform and would reduce your search time for the previous algorithm.

Alternatively

You could simply do a real Dijkstra's algorithm between each set of points, pathing out the closest points first (or trying them in some random orders a few times). This would probably work for a fair number of cases, and when it fails simply throw out the map and generate a new one.

Once you have Step 1 solved, Step 2 should be easier, though not necessarily trivial. To grow your paths, I think you'll want to grow your paths outward (so paths closest to walls first, growing towards the walls, then other inner paths outwards, etc.). To grow, I think you'll have two basic operations, flipping corners, and expanding into into adjacent pairs of empty squares.. that is to say, if you have a line like

.v<<.
v<...
v....
v....

First you'll want to flip the corners to fill in your edge spaces

v<<<.
v....
v....
v....

Then you'll want to expand into neighboring pairs of open space

v<<v.
v.^<.
v....
v....

v<<v.
>v^<.
v<...
v....

etc..

Note that what I've outlined wont guarantee a solution if one exists, but I think you should be able to find one most of the time if one exists, and then in the cases where the map has no solution, or the algorithm fails to find one, just throw out the map and try a different one :)

The most straightforward way to create such a level is to find a way to solve it. This way, you can basically generate any random starting configuration and determine if it is a valid level by trying to have it solved. This will generate the most diverse levels.

And even if you find a way to generate the levels some other way, you'll still want to apply this solving algorithm to prove that the generated level is any good ;)

Brute-force enumerating

If the board has a size of NxN cells, and there are also N colours available, brute-force enumerating all possible configurations (regardless of wether they form actual paths between start and end nodes) would take:

N^2 cells total
2N cells already occupied with start and end nodes
N^2 - 2N cells for which the color has yet to be determined
N colours available.
N^(N^2 - 2N) possible combinations.

So,

For N=5, this means 5^15 = 30517578125 combinations.
For N=6, this means 6^24 = 4738381338321616896 combinations.

In other words, the number of possible combinations is pretty high to start with, but also grows ridiculously fast once you start making the board larger.

Constraining the number of cells per color

Obviously, we should try to reduce the number of configurations as much as possible. One way of doing that is to consider the minimum distance ("dMin") between each color's start and end cell - we know that there should at least be this much cells with that color. Calculating the minimum distance can be done with a simple flood fill or Dijkstra's algorithm. (N.B. Note that this entire next section only discusses the number of cells, but does not say anything about their locations)

In your example, this means (not counting the start and end cells)

dMin(orange) = 1
dMin(red) = 1
dMin(green) = 5
dMin(yellow) = 3
dMin(blue) = 5

This means that, of the 15 cells for which the color has yet to be determined, there have to be at least 1 orange, 1 red, 5 green, 3 yellow and 5 blue cells, also making a total of 15 cells. For this particular example this means that connecting each color's start and end cell by (one of) the shortest paths fills the entire board - i.e. after filling the board with the shortest paths no uncoloured cells remain. (This should be considered "luck", not every starting configuration of the board will cause this to happen).

Usually, after this step, we have a number of cells that can be freely coloured, let's call this number U. For N=5,

U = 15 - (dMin(orange) + dMin(red) + dMin(green) + dMin(yellow) + dMin(blue))

Because these cells can take any colour, we can also determine the maximum number of cells that can have a particular colour:

dMax(orange) = dMin(orange) + U
dMax(red)    = dMin(red) + U
dMax(green)  = dMin(green) + U
dMax(yellow) = dMin(yellow) + U
dMax(blue)   = dMin(blue) + U

(In this particular example, U=0, so the minimum number of cells per colour is also the maximum).

Path-finding using the distance constraints

If we were to brute force enumerate all possible combinations using these color constraints, we would have a lot less combinations to worry about. More specifically, in this particular example we would have:

  15! / (1! * 1! * 5! * 3! * 5!)
= 1307674368000 / 86400
= 15135120 combinations left, about a factor 2000 less.

However, this still doesn't give us the actual paths. so a better idea would be to a backtracking search, where we process each colour in turn and attempt to find all paths that:

doesn't cross an already coloured cell
Is not shorter than dMin(colour) and not longer than dMax(colour).

The second criteria will reduce the number of paths reported per colour, which causes the total number of paths to be tried to be greatly reduced (due to the combinatorial effect).

In pseudo-code:

function SolveLevel(initialBoard of size NxN)
{
    foreach(colour on initialBoard)
    {
        Find startCell(colour) and endCell(colour)
        minDistance(colour) = Length(ShortestPath(initialBoard, startCell(colour), endCell(colour)))
    }

    //Determine the number of uncoloured cells remaining after all shortest paths have been applied.
    U = N^(N^2 - 2N) - (Sum of all minDistances)

    firstColour = GetFirstColour(initialBoard)
    ExplorePathsForColour(
        initialBoard, 
        firstColour, 
        startCell(firstColour), 
        endCell(firstColour), 
        minDistance(firstColour), 
        U)
    }
}

function ExplorePathsForColour(board, colour, startCell, endCell, minDistance, nrOfUncolouredCells)
{
    maxDistance = minDistance + nrOfUncolouredCells
    paths = FindAllPaths(board, colour, startCell, endCell, minDistance, maxDistance)

    foreach(path in paths)
    {
        //Render all cells in 'path' on a copy of the board
        boardCopy = Copy(board)
        boardCopy = ApplyPath(boardCopy, path)

        uRemaining = nrOfUncolouredCells - (Length(path) - minDistance)

        //Recursively explore all paths for the next colour.
        nextColour = NextColour(board, colour)
        if(nextColour exists)
        {
            ExplorePathsForColour(
                boardCopy, 
                nextColour, 
                startCell(nextColour), 
                endCell(nextColour), 
                minDistance(nextColour), 
                uRemaining)
        }
        else
        {
            //No more colours remaining to draw
            if(uRemaining == 0)
            {
                //No more uncoloured cells remaining
                Report boardCopy as a result
            }
        }
    }
}

FindAllPaths

This only leaves FindAllPaths(board, colour, startCell, endCell, minDistance, maxDistance) to be implemented. The tricky thing here is that we're not searching for the shortest paths, but for any paths that fall in the range determined by minDistance and maxDistance. Hence, we can't just use Dijkstra's or A*, because they will only record the shortest path to each cell, not any possible detours.

One way of finding these paths would be to use a multi-dimensional array for the board, where each cell is capable of storing multiple waypoints, and a waypoint is defined as the pair (previous waypoint, distance to origin). The previous waypoint is needed to be able to reconstruct the entire path once we've reached the destination, and the distance to origin prevents us from exceeding the maxDistance.

Finding all paths can then be done by using a flood-fill like exploration from the startCell outwards, where for a given cell, each uncoloured or same-as-the-current-color-coloured neigbour is recursively explored (except the ones that form our current path to the origin) until we reach either the endCell or exceed the maxDistance.

An improvement on this strategy is that we don't explore from the startCell outwards to the endCell, but that we explore from both the startCell and endCell outwards in parallel, using Floor(maxDistance / 2) and Ceil(maxDistance / 2) as the respective maximum distances. For large values of maxDistance, this should reduce the number of explored cells from 2 * maxDistance^2 to maxDistance^2.

Consider solving your problem with a pair of simpler, more manageable algorithms: one algorithm that reliably creates simple, pre-solved boards and another that rearranges flows to make simple boards more complex.

The first part, building a simple pre-solved board, is trivial (if you want it to be) if you're using n flows on an nxn grid:

For each flow...
- Place the head dot at the top of the first open column.
- Place the tail dot at the bottom of that column.

Alternatively, you could provide your own hand-made starter boards to pass to the second part. The only goal of this stage is to get a valid board built, even if it's just trivial or predetermined, so it's worth keeping it simple.

The second part, rearranging the flows, involves looping over each flow, seeing which one can work with its neighboring flow to grow and shrink:

For some number of iterations...
- Choose a random flow f.
- If f is at the minimum length (say 3 squares long), skip to the next iteration because we can't shrink f right now.
- If the head dot of f is next to a dot from another flow g (if more than one g to choose from, pick one at random)...
  - Move f's head dot one square along its flow (i.e., walk it one square towards the tail). f is now one square shorter and there's an empty square. (The puzzle is now unsolved.)
  - Move the neighboring dot from g into the empty square vacated by f. Now there's an empty square where g's dot moved from.
  - Fill in that empty spot with flow from g. Now g is one square longer than it was at the beginning of this iteration. (The puzzle is back to being solved as well.)
- Repeat the previous step for f's tail dot.

The approach as it stands is limited (dots will always be neighbors) but it's easy to expand upon:

Add a step to loop through the body of flow f, looking for trickier ways to swap space with other flows...
Add a step that prevents a dot from moving to an old location...
Add any other ideas that you come up with.

The overall solution here is probably less than the ideal one that you're aiming for, but now you have two simple algorithms that you can flesh out further to serve the role of one large, all-encompassing algorithm. In the end, I think this approach is manageable, not cryptic, and easy to tweek, and, if nothing else, a good place to start.

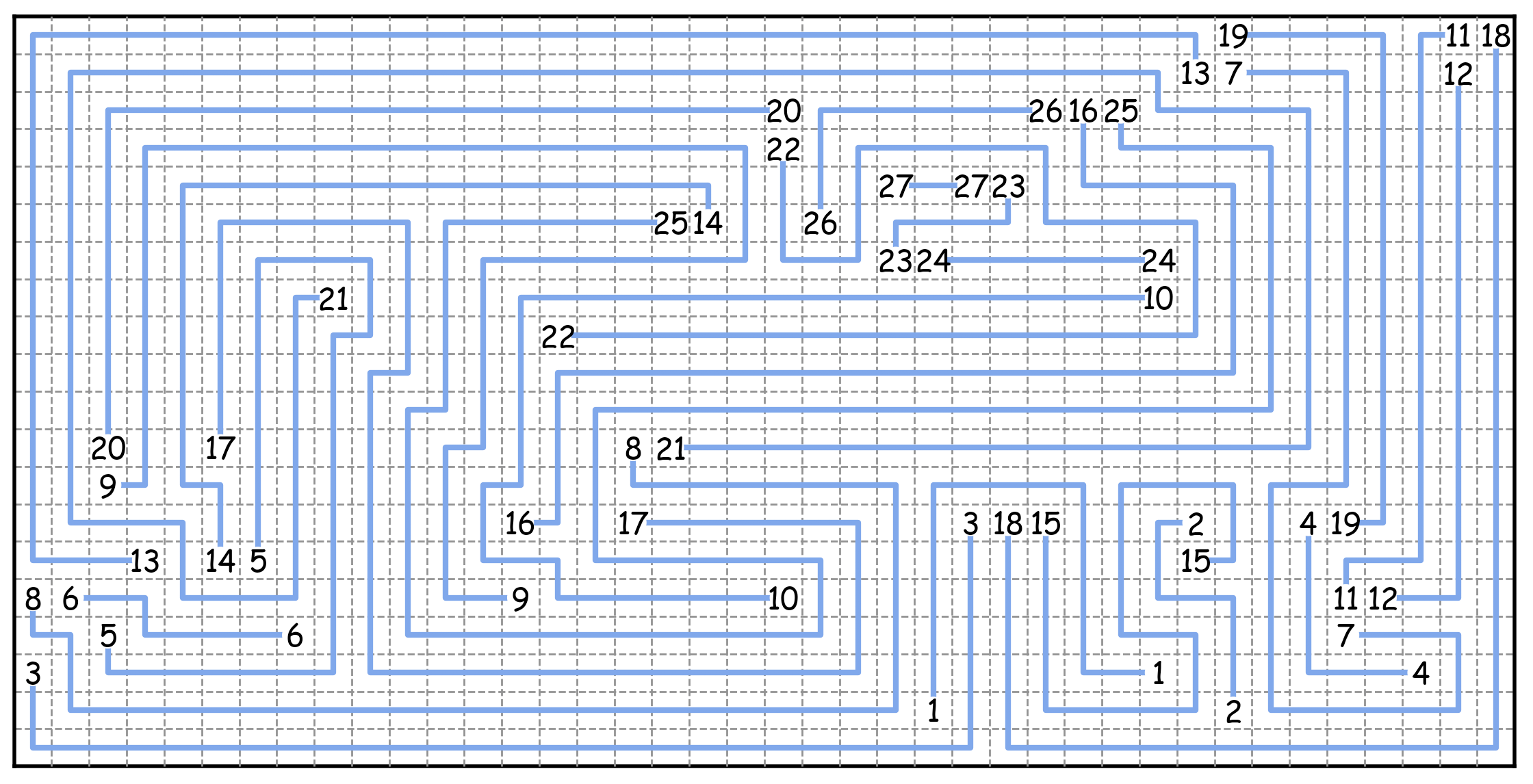
Update: I coded a proof-of-concept based on the steps above. Starting with the first 5x5 grid below, the process produced the subsequent 5 different boards. Some are interesting, some are not, but they're always valid with one known solution.

Starting Point
Image 1 - starting frame