How many unit cylinders can touch a unit ball?
Here is an idea. Consider the following parameterization, which is supposed to cover the configuration space in question.
$$\mathcal{C}_7:=\left\{\pmatrix{x_k\\y_x\\z_k},\pmatrix{a_k\\b_k\\c_k}_{1\leq k\leq 7}\in{\mathbb{R}^{3\times 2}}^7\,\middle |\, \text{such that conditions 1.-4. are satisfied} \right\} $$
Conditions:
- $x_k^2+y_k^2+z_k^2=1$
- $\left\langle\pmatrix{x_k\\y_k\\z_k},\pmatrix{a_k\\b_k\\c_k} \right\rangle=0$
- $a_k^2+b_k^2+c_k^2=1$
- $d(l_i,l_j)\geq 2$ for $1\leq i<j\leq 7,$ where we define the line $$l_k:=\left\{2\pmatrix{x_k\\y_k\\z_k}+\alpha\pmatrix{a_k\\b_k\\c_k}\,\middle|\,\alpha\in\mathbb{R} \right\}$$ and denote with $d(\cdot,\cdot)$ the distance between two lines.
Note that condition 4. can be rewritten as polynomial inequalities. Hence $\mathcal{C}_7$ is a semi-algebraic set in $\mathbb{R}^{42}$.
The $(x,z,y)$ are the points, where the unit cylinder is tangent to the unit sphere. The corresponding $(a,b,c)$ gives the direction in the tangent space and the lines $l$ are the cores of the cylinders. (Note that $(-a,-b,-c)$ gives the same cylinder.)
The question "Is $\mathcal{C}_7$ empty?" should be decidable. Maybe an algorithmic approach could help from here.
For the other questions the study of an analogues defined $\mathcal{C}_6$, which we know to be non-empty might be worthwhile.
I wrote a little program that tries to find points in the described semi-algebraic sets. Here's what it found for $\mathcal{C}_6$ (click here for an animation).
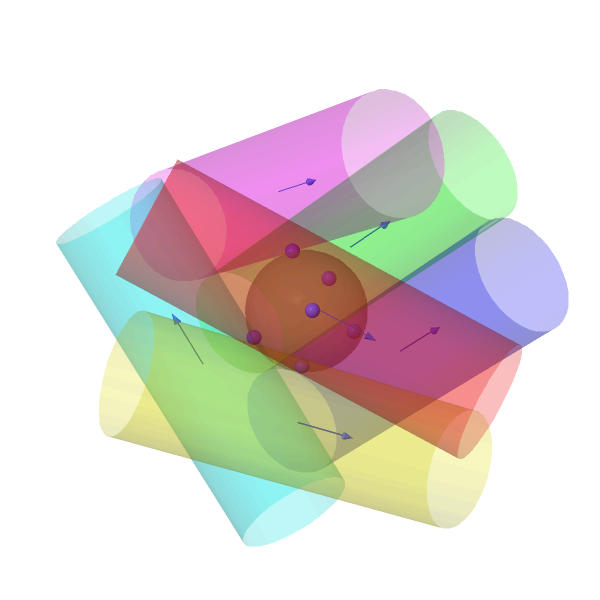
Let's take a slightly different point of view. Fix the radius of the ball to be $1$, but let the radii of the $k$ cylinders vary while making sure all cylinders have the same radius. We can then ask: What is the largest radius $r_k$, so that we can find $k$ non-overlapping cylinders of radius $r_k$, that touch the unit ball? Hence the question is: $r_7\geq 1?$
An obvious lower bound on $r_k$ comes from the packing that allows a equatorial section which is a circle packing, as for $k=6$ in figure 1 and figure 2 in the question post. We therefore have:
$$r_k\geq \frac{\operatorname{sin}(\frac{\pi}{k})}{1-\operatorname{sin}(\frac{\pi}{k})}$$
Here's a list of decimal approximations for small $k$s:
$$\begin{array}{c|cccccc}k&3&4&5&6&7&8\\\hline
\frac{\operatorname{sin}(\frac{\pi}{k})}{1-\operatorname{sin}(\frac{\pi}{k})}
&6.464101& 2.414213& 1.425919& 1&
0.766421& 0.619914\end{array}$$
A perhaps surprising result of my calculations is the fact that $r_6>1$, indeed
$$r_6> 1.04965$$
So in other words there is configuration of $6$ cylinders where the cylinders have radius larger than $1.04965$. Here is a picture of the configuration
(again click here for an animation):

I also drew cylinders of radius $1$ with the same tangent points, so one can see the difference.
The configuration space can be viewed as subset of the the $6$th power of the unit tangent bundle of the sphere $(T^1(S^2))^6$ (see conditions 1.-4. and Henrik Rüping's comment).
The upshot of finding a configuration with larger radius is: the configuration space contains an open subset of $(T^1(S^2))^6$ and hence is $18$-dimensional locally.
Edit:
Here is list of lower bounds on $r_k$ for small $k$:
- For $k=3$ and $k=4$ I conjecture the trivial bound for $r_k$ given above to be sharp.
- For $k=5$ one can find a configuration that shows: $r_5>1.45289>1.425919$
- For $k=6$ we have $r_6>1.04965 >1$ as mentioned above.
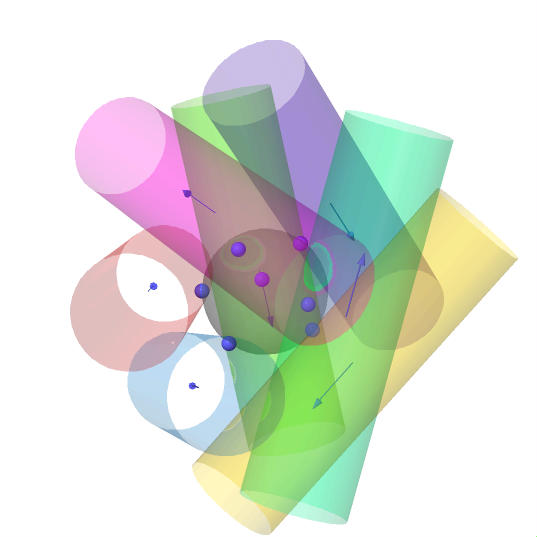
- For $k=7$ I found a configuration that shows $r_7>0.846934>0.766421$. Here is a picture of this configuration (again click here for an animation):
For a javascript rendered 3D model of the path of configurations reported by Ogievetsky and Shlosman in arXiv:1805.09833 see this page on my website.
The configurations in this path are composed of two "three-pole teepees" pointed in antipodal directions. This is also true of the Figure 3 configuration in the question. But a crucial difference is that in Ogievetsky and Shlosman's configurations, the two teepees are both right-handed. In Figure 3, the two teepees have different handedness.
You can set up the calculation of OS in the case of opposite-handed teepees. Just switch $\delta$ to $-\delta$ for $D$, $E$, and $F$ in their Equation (5). Now solving for $d_{AB}=d_{AD}=d_{BD}$ is even easier. From $d_{AD}=d_{BD}$ I get $\varkappa=0$, and from $d_{AB}=d_{AD}$, I get $$s+\frac{3(s-1)}{t+4-3s}+\frac{s-s^2}{s+t}=0\text,$$ where $s=(\sin\phi)^2$ and $t=(\tan\delta)^2$.
There are two real solutions for $t$ when $0\le s\le \tfrac13$, and then the solutions become complex for $\tfrac13<s\le1$. All the real solutions give $d_{AB}=d_{AD}=d_{BD}\le1$, with equality only for the double solution $s=\tfrac13$, $t=1$, which is Figure 3.
This is not a complete answer, but a suggestion of approach to prove that the configuration shown in figure 3 is locked. I hope it is not to naive.
We consider a continuous perturbation of the configuration and want to prove it is obtained by applying a continuous deformation of identity in $\mathrm{SO}(3)$.
Step 1: look at two opposite cylinders, and show that their contact points with the sphere must stay antipodal. This should hold because otherwise one of the other four cylinders would probably not have enough room left.
Step 2: consider again two opposite cylinders, and show that they stay parallel. This should hold because of step 1: we can assume that their contact points with the sphere are fixed, and then if they rotate in opposite direction then another pair of opposite cylinders must also rotate in opposite directions, which in turns constrains the movement of the last pair; if I am right, this last pair in turn constrains the first pair to twist in the opposite direction it does twist. In this argument, I guess that the parity of the dimension matters, so the $4$-dimensional version of the problem could have a different solution.
Step 3: conclude the proof. We can assume that a given pair of opposite cylinders is fixed; then the second pair is constrained to rotate in the plane containing its axes (at least at first order), which rotation is prevented by the third pair.