Is The *Mona Lisa* in the complement of the Mandelbrot set.
I think yes
Consider the sequence of "westernmost" islands increasing in period:
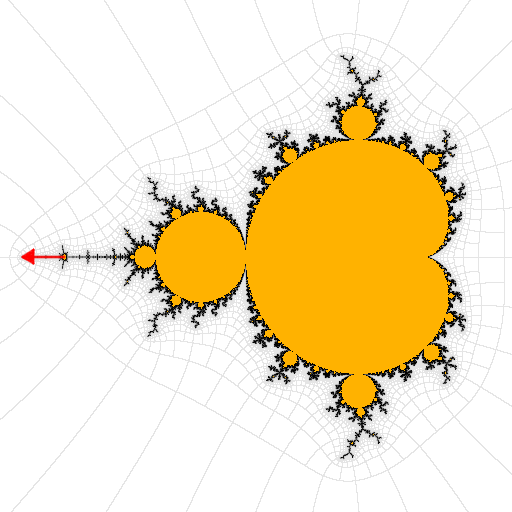
Here are some examples, you can see them increasing in hairyness / spinyness.
Period 20:

Period 30:

Period 40:

Period 50:

Zooming in near to a sufficiently hairy high-period island, you can get very nearly parallel spines:
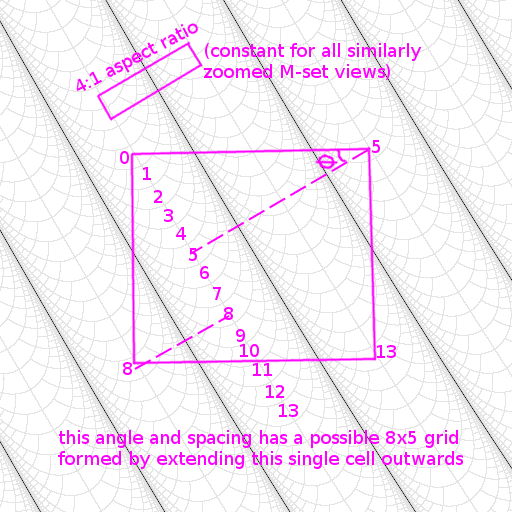
There is a natural grid with a 4:1 aspect ratio between successive escape time level sets in neighbouring spine gaps. (Determined by measuring images: I have no proof of this seeming fact. But it's not a strictly necessary detail.)
If you choose the angle of the spines carefully, you can create an NxN grid with square cells that satisfies "distinct level set at each pixel sampling point in an (m,n) image array".
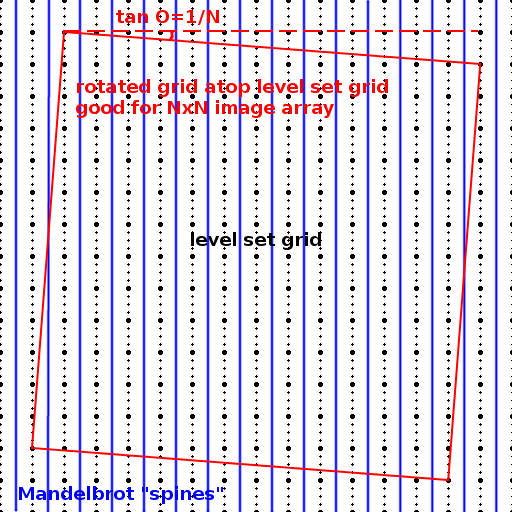
There is a slight fuzziness due to the imperfect parallelism and the quantized angles available for any given period island, but increasing the period far enough and that won't matter - eventually it gets good enough for the finite width of the level sets to take care of it.