Trying to visualize the Collatz conjecture

If you want to make several sequences of the Collatz function for turning it into a graph, you probably want to memorize, which parts you already calculated. What we try to do is to create a graph like this (image from xkcd):

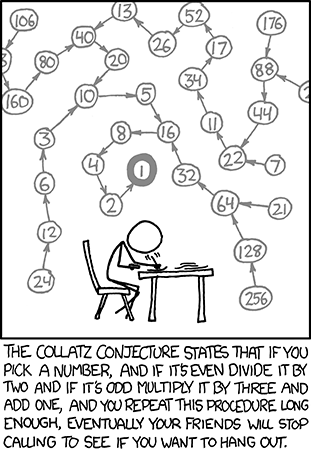
When we would calculate the whole chain for each number until it (hopefully) reaches the end sequence 8,4,1 we do a lot of work over and over again. Therefore, we want an algorithm that when calculating 24 stops at 10 if this chain has already be calculated.

A moderately understandable solution is to use a Module that contains a function which is used as memory to store, whether a numbers was already seen. Additionally, we use a Internal`Bag to store all the different chains. The following function takes a list of positive numbers and calculates the Collatz-sequence for each number. It stops each sequence, when it meets a number that has already be seen:

CollatzSequence[list_] := Module[{memory, tmp, chain, result = Internal`Bag[]},

  memory[1] = False;
  memory[n_] := (memory[n] = False; True);

  Do[
   chain = Internal`Bag[];
   tmp = l;
   While[memory[tmp],
    Internal`StuffBag[chain, tmp];
    tmp = If[EvenQ[tmp], tmp/2, 3 tmp + 1];
    ];
   Internal`StuffBag[chain, tmp];
   Internal`StuffBag[result, chain],
   {l, list}];
  Internal`BagPart[#, All] & /@ Internal`BagPart[result, All]
]

CollatzSequence[{10, 11, 12}]
(* {{10, 5, 16, 8, 4, 2, 1}, {11, 34, 17, 52, 26, 13, 40, 20, 
  10}, {12, 6, 3, 10}} *)

This can now easily be used to create a Graph. It works even for a very large number of chains like say 50000. The only thing you have to do is to turn the list of numbers into list of edges:

Graph[
 Flatten[(Rule @@@ Partition[#, 2, 1]) & /@ 
   CollatzSequence[Range[50000]]],
 PerformanceGoal -> "Speed", 
 GraphLayout -> {"PackingLayout" -> "ClosestPacking"}, 
 VertexStyle -> Opacity[0.2, RGBColor[44/51, 10/51, 47/255]], 
 EdgeStyle -> RGBColor[38/255, 139/255, 14/17]]

---

Another very nice way to visualize Collatz-sequences is to draw them as path which makes left/right turns depending on the whether the number is odd or even. I got inspired by a reddit post and wrote my own version that uses this color scheme. The results look stunningly beautiful

Only for reference, let me give you my uncleaned code for a small Manipulate that lets you change everything live.

SetAttributes[Collatz, {Listable}];
Collatz[n_, e_, a_, f_] := Module[{nn = n, bag = Internal`Bag[]},
   While[nn =!= 1, Internal`StuffBag[bag, nn];
    nn = If[EvenQ[nn], nn/2, 3 nn + 1]
    ];
   Internal`StuffBag[bag, nn];
   With[{seq = Reverse[Internal`BagPart[bag, All]]}, 
    AnglePath[Transpose[{seq/(1 + seq^e), a*(f - 2 Mod[seq, 2])}]]]];

astroIntensity[l_, s_, r_, h_, g_] := 
  With[{psi = 2 Pi (s/3 + r l), a = h l^g (1 - l^g)/2}, 
   l^g + a*{{-0.14861, 1.78277}, {-0.29227, -0.90649}, {1.97294, 
        0.0}}.{Cos[psi], Sin[psi]}];

Manipulate[
 DynamicModule[{seq},
  seq = ControlActive[Collatz[Range[5000, 5020], e, a, f], 
    Collatz[RandomInteger[1000000, {n}], e, a, f]];
  Graphics[{Opacity[o], Thickness[ControlActive[0.01, 0.003]], 
    Line[seq, 
     VertexColors -> (Table[
          astroIntensity[l, s, r, h, g], {l, 0, 1, 
           1/(Length[#] - 1)}] & /@ seq)]}, ImageSize -> 500]
  ]
 , "Colors", {{s, 2.49}, 0, 3}, {{r, 0.76}, 0, 5}, {{h, 1.815}, 0, 
  2}, {{g, 1.3}, 0.1, 2}, {{o, 0.5}, 0.1, 1},
 Delimiter,
 "Structure",
 {{e, 1.3}, 0.9, 1.8},
 {{a, 0.19}, 0.1, 0.3},
 {{f, 0.7}, 0.1, 1.5},

 {n, 300, 5000, 1}
 ]

Many more Collatz visualization strategies and analysis algorithms can be found in this blog post of user vzn.

This is the Collatz function I know:

Collatz[1] := {1}
Collatz[n_Integer]  := Prepend[Collatz[3 n + 1], n] /; OddQ[n] && n > 0
Collatz[n_Integer] := Prepend[Collatz[n/2], n] /; EvenQ[n] && n > 0

Generating a graph from this is easy:

Graph[(DirectedEdge @@@ Partition[Collatz[#], 2, 1]) & /@ Range[500] // Flatten // Union, 
 EdgeShapeFunction -> GraphElementData[{"Arrow", "ArrowSize" -> .005}], 
 GraphLayout -> "LayeredDrawing"]

or with a different layout and with labeling:

Graph[(DirectedEdge @@@ Partition[Collatz[#], 2, 1]) & /@ Range[100] //
    Flatten // Union, GraphLayout -> "RadialEmbedding", 
 VertexLabels -> "Name"]

A very fast version using memoization:

Collatz[1] := {1}
Collatz[n_Integer] := Collatz[n] = Prepend[Collatz[3 n + 1], n] /; OddQ[n] && n > 0
Collatz[n_Integer] := Collatz[n] = Prepend[Collatz[n/2], n] /; EvenQ[n] && n > 0

For a range of the first 5000 integers this gives a speedup of about a factor of 250. You might want to do a ClearAll[Collatz] afterwards to cleanup memory from all the stored chains.