What is higher dimensional algebra?
Ordinary algebra (monoids and their linear cousins rings) involves an operation that's written on a line. That is, you can multiple on the left or on the right. It's 1-dimensional algebra.
Higher dimensional algebra is algebra where it's more natural to write your operations on a higher dimensional manifold. For example, the Temperley-Lieb algebra is naturally 2-dimensional. You can multiple on the left, right, top, or bottom. Similarly Hopf algebras can be thought of as 2-dimensional, with the coproduct being related to multiplication in a different dimension.
Asking for a rigorous definition of "higher dimensional algebra" is counterproductive. It's a subject, not a mathematical object. But one way of making it more precise would be to say that higher dimensional algebra is the study of n-categories. Again, I think that last sentence is misleading, but at least n-categories are something you can look up definitions of.
A good place to start reading about higher dimensional algebra is going through back issues of this week in mathematical physics.
My definition of higher dimensional algebra is that it is the study and application of algebraic theories with partial algebraic structures whose domains are defined by geometric conditions. I think the first study of such partial algebraic structures was in Higgins, P.~J. "Algebras with a scheme of operators". Math. Nachr. 27 (1963) 115--132.
The intuitive idea is also: do mathematical formulae have to be confined to a line? Can we have and use formulae in 2 or 3 or many dimensions? and can this be useful? If so we can expect to need rewriting of such formulae, and indeed this exists and is useful. You can find many 2-dimensional rewrites in the new book Nonabelian Algebraic Topology (European Mathematical Society, 2011), and with a pdf available. See for example the rotations in section 6.4, used in this mathoverflow answer on computing homotopies.
Those who have read Flatland will remember that the Linelanders had a rather limited existence! Can we really think that the brain works in one dimension only?
I mention that the idea of all this occurred to me in 1965 when I thought that the proof I had written out many times for the van Kampen Theorem for the fundamental groupoid should generalise to higher dimensions, if one had the right gadgets, seen as higher homotopy groupoids. 9 years later: whoopee! (work with Chris Spencer and with Philip Higgins). The first joint papers with Philip were published in 1978 and 1981.
Note that group objects in the category of groups are just abelian groups. But double groupoids, which are groupoid objects in the category of groupoids, are much more complicated than groups, and can model $2$-dimensional homotopical notions.
You can find presentations on some of these ideas on my preprint page, and including a presentation Theoretical Neuroscience in Delhi in 2003, which went down well! arXiv:math/0306223.
For my purposes I have needed a cubical context, which is not commonly followed, but in which it was easier to conjecture and prove the theorems I was thinking of. But the definition above seems quite general, and allows for a melding of algebra and geometry.
I also believe that Henry Whitehead's term `Combinatorial homotopy' and his actual work show he was thinking of generalising some methods of combinatorial group theory to higher dimensions. His notion of crossed module (1946) has proved an important feature of such ideas, and crossed modules later appeared in a key relations with $2$-groups and more generally with double groupoids.
In another direction the following diagram
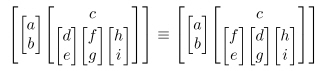
occurs in this paper on double semigroups.
I'll use this question as an opportunity to advertise a notion of "two-dimensional algebra" from my paper http://arxiv.org/pdf/0912.5307v2.
Definition:
A 2-algebra consists of a vector space $A$, two bilinear operations
$$
a,b\mapsto ab\qquad\qquad\qquad\text{and}\qquad\qquad\qquad a,b\mapsto\, \begin{matrix} a\\ b\end{matrix}
$$
and three distinguished elements $1$, $v$, and $v^{-1}$, subject to the axioms
• $\qquad 1a=a=a1$
• $\qquad (ab)c=a(bc)$
• $\qquad \begin{matrix}\stackrel{\displaystyle (ab)}{(cd)}\end{matrix}
=\big(\begin{matrix}\stackrel{\displaystyle a}{c}\end{matrix}\big)\big(\begin{matrix}\stackrel{\displaystyle b}{d}\end{matrix}\big)
$
• $\qquad v\Big(\begin{matrix}(\begin{matrix}\stackrel{\displaystyle a}{b}\end{matrix})\\\ c\end{matrix}\Big)v^{-1}=\Big(
\begin{matrix}a\\\ (\begin{matrix}\stackrel{\displaystyle b}{c}\end{matrix})\end{matrix}\Big)$
• $\qquad vv=(\begin{matrix}\stackrel{\displaystyle 1}{v}\end{matrix})v(\begin{matrix}\stackrel{\displaystyle v}{1}\end{matrix})$
• $\qquad vv^{-1}=v^{-1}v=1$