Closed-form expression for certain product

the OP asks for some numerical evidence: plotted below is the constant $\alpha$ minus the $\prod_{n=1}^N$ of the expression in OP, as a function of $N$; so at least within 1 part in 1000 the infinite product does seem to converge from above to the stated constant.

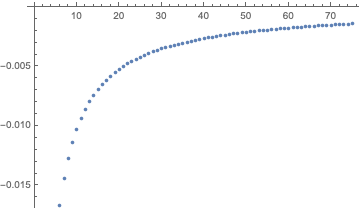
Using the Maple code from user64494's answer (but using mul(evalf(...)) instead of evalf(product(...)) for greater efficiency, and 20 digits), I computed the product for 1000,2000,3000,4000 terms. It took about four minutes.

The answers were: 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236.

Now assuming that the product to $N$ terms has an asymptotic expansion $$a_0+a_1/N+a_2/N^2+a_3/N^3+\cdots,$$ which can surely be proved but I didn't, extrapolation of these 4 values gives $$a_0\approx 0.7804591974129376479,a_1\approx 0.107, a_2\approx -0.0463, a_3\approx 0.0151.$$ The value of $a_0$ agrees with the proposed infinite product 0.7804591974129374862 to 15 digits.

ADDED: By evaluating $x^x$ as evalf(x)^x, the same computation runs in about 20 seconds even with twice the precision. Adding the product with 5000 terms, agreement to 20 digits is obtained.

ADDED[2]: I don't know how it does it, but Maple's built-in code for numerical evaluation of infinite products takes mere seconds to confirm this to 200 digits.

The following Mathematica code

NProduct[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n - 
  1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n - 
  7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n - 
  1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -13/20)^(n -13/20)/
((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n - 
       1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
       n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 + 
      n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 + 
     n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)),
{n,1,Infinity}, AccuracyGoal -> 3, WorkingPrecision -> 15]

performs

$0.78046 $

If somebody verifies the above code, it would be kind of her/him.

Addition. The Maple command for the product up to $100$

Digits:=15:evalf(product((1/2+n)^(1/2+n)*(7/12+n)^(7/12+n)*(1/20+n)^(1/20+n)*(13/20+n)^(13/20+n)*(n-1/4)^(n-1/4)*(n-1/12)^(n-1/12)*(n-11/20)^(n-11/20)*(n-3/20)^(n-3/20)/(exp(1)*n*(n-1/2)^(n-1/2)*sqrt(exp(1)*n)*(n-7/12)^(n-7/12)*(n-1/20)^(n-1/20)*(n-13/20)^(n-13/20)*(1/4+n)^(1/4+n)*(1/12+n)^(1/12+n)*(11/20+n)^(11/20+n)*(3/20+n)^(3/20+n)), n = 1 .. 100));

produces $0.781527175985084 $.

Also

N[Exp[47*Catalan/30/Pi + 3/4]*  Sqrt[33/91/Pi*Sqrt[2/Pi*11^(1/5)/7^(1/3)*3^(3/5)/13^(3/5)]], 15]

$0.780459197412937 $

Edit. A typo in the codes ($(n-1/2)^{n-1/2}$ instead of $(n-1/2)^{n-1}$) is corrected. That typo leads to incorrect results.